ciagi Kamil: Niech f(x) = 1 + x + x² + x³ + ... będzie sumą szeregu geometrycznego zbieżnego. Udowodnij, że zbiorem wartości funkcji f jest przedział (¹₂ , +∞) . Doszedłem do miejsca, gdzie wyznaczam |q|<1, co za tym idzie x ∊ (−1, 1). Niestety nie wiem jak to dalej ruszyć, prosze o pomoc

Metis: Oblicz sumę , potraktuj ją jako funkcję i pokaż, że zbiorem wartości jest podany przedział.

Janek191:

	1
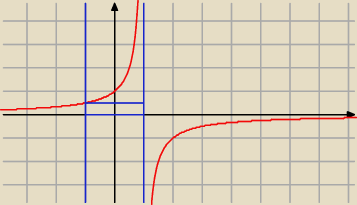
f(x) =		; I x I < 1
	1 − x

	1		1
f ( − 1) =		= −
	1 − (−1)		2

lim f(x) = +∞ x→1⁻

Kamil: Tak też zrobiłem i wyszło mi f(x) = ¹_1−x . Co dalej? Wydaję się to być proste, ale jakoś nie mogę na to wpaść..

Kamil: Ooooooo, teraz jasne, wielkie dzięki Janek !

Janek191:

	1
Tam jest pomyłka − powinno być f( −1) =
	2

Kamil: Tylko tak sobie myślałem, że już wszystko pięknie rozumiem, aż tu nagle przyszła pewna myśl, dlaczego licze f dla x = −1?

Janek191: Dziedzina : x ∊ ( − 1, 1)