Stereometria, oblicz odległość. Kebab: "Oblicz odległość środka ściany sześcianu od przekątnej tego sześcianu, jeżeli jego objętość wynosi V." Nie mam pojęcia jak to nawet sobie wyobrazić

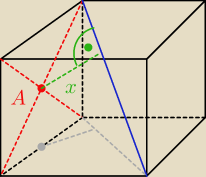
kochanus_niepospolitus: Szukasz 'x' Na szaro zaznaczyłem 'rzut na podstawę' przekątnej sześcianu, środka ściany i szukanej odległości. Równie dobrze możesz zacząć od obliczenia tych właśnie długości (rzutów na podstawę), będzie łatwiej Ci wyobrazić sobie jak wyglądają trójkąty prostokątne ... a na koniec po prostu skorzystać z podobieństwa trójkątów (po wcześniejszym wyznaczeniu 'skali podobieństwa' wyliczając 'dłuższą część przekątnej'

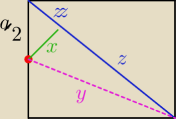kochanus_niepospolitus: niech bok = a (czyli a³ = V ... więc a = ³√V) wtedy:

	a
y = √a2 + a2/4 =		√5
	2

i mamy: zz + z = a√2 −> zz = a√2 − z z tw. Pitagorasa: x² + z² = y²

	a
(zz)2 + x2 = (		)2
	2

z tego wyjdzie:

	y√2		a√2
x =		=
	2√5		4

	3y√2		3a√2
z =		=
	2√5		4

Pamiętaj, że są to wartości 'na podstawie' ... teraz musisz je 'przerobić w 3D' (tak wiem ... mało 'matematycznie' to napisałem )

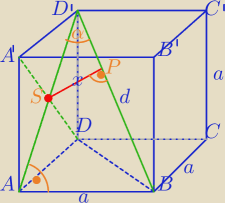Mila: V=a³ a=³√V ==== d=a√3 |AD'|=a√2 ΔSPD'∼ΔBAD'⇔

x		a
	=		⇔x*d=|SD'|*a
|SD'|		d

	a√2
x*a√3=		*a⇔
	2

	a√2
x*√3=		/*√3
	2

	a√6
3x=		/:3
	2

	a√6
x=
	6

podstaw za a i dokończ ==================