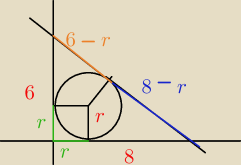
 Poprowadzono trzy styczne do okręgu. Każde dwie z tych stycznych przecinają się w jednym
punkcie. Punkty te tworzą trójkąt prostokątny o przyprostokątnych długości 6 i 8, który
opisany jest na danym okręgu. Oblicz długość promienia tego okręgu.
Wydaje mi się, że dobrze zrobiłam to zadanie, jednak moja odpowiedź nie do końca zgadza się z
tą podręcznikową. Proszę o wskazanie błędu w moich obliczeniach
Moje obliczenia są takie:
Założenia:
r>0
6−r>0 r<6
8−r>0 r<8
Obliczenia:
c = (6−r)+(8−r) = 14−2r
62+82 = (14−2r)2
36+64 = 196−56r+4r2
100 = 196−56r+4r2 | −100
0 = 96−56r+4r2 | :4
r2−14r+24 = 0
Δ = (−14)2 − 4*1*24
Δ = 100
√Δ = 10
r1 = 14−102 = 2
r2 = 14+102 = 12 <− Odpada, bo r<6
a więc r = 2
W podręczniku jednak odpowiedź to r=2 lub r=4 lub r=6 lub r=12.. Dlaczego, skoro r<6 ? i skąd
wzięło się r=4?
Poprowadzono trzy styczne do okręgu. Każde dwie z tych stycznych przecinają się w jednym
punkcie. Punkty te tworzą trójkąt prostokątny o przyprostokątnych długości 6 i 8, który
opisany jest na danym okręgu. Oblicz długość promienia tego okręgu.
Wydaje mi się, że dobrze zrobiłam to zadanie, jednak moja odpowiedź nie do końca zgadza się z
tą podręcznikową. Proszę o wskazanie błędu w moich obliczeniach
Moje obliczenia są takie:
Założenia:
r>0
6−r>0 r<6
8−r>0 r<8
Obliczenia:
c = (6−r)+(8−r) = 14−2r
62+82 = (14−2r)2
36+64 = 196−56r+4r2
100 = 196−56r+4r2 | −100
0 = 96−56r+4r2 | :4
r2−14r+24 = 0
Δ = (−14)2 − 4*1*24
Δ = 100
√Δ = 10
r1 = 14−102 = 2
r2 = 14+102 = 12 <− Odpada, bo r<6
a więc r = 2
W podręczniku jednak odpowiedź to r=2 lub r=4 lub r=6 lub r=12.. Dlaczego, skoro r<6 ? i skąd
wzięło się r=4?
| 2P | ||
Zadanie na jedną linijkę ...liczysz c i pole r = | = 2 | |
| a+b+c |
