matura Metis: Maturka... Cześć Możecie sprawdzić mi moją maturkę? Nie mam do niej odpowiedzi. Arkusz : http://zamosc.lscdn.pl/download/2/18226/ArkuszPRLSCDN2016kl3LO.pdf Lubelska próba przed matura 2016 PR. Zadania od 1−5: > http://i.imgur.com/PA7AZ5A.png Ich rozwiązania: > http://i.imgur.com/0u5RUkT.jpg Zad.6: http://i.imgur.com/XaSDcSk.jpg Zad.7: nie poradziłem z Nim sobie Eta? Zad.8: http://i.imgur.com/J7rLPqb.jpg Zad.9 Tutaj też nie ma rozwiązania, ale pierwsze na co wpadłem to doprowadzenie do równania kwadratowego , ale coś nie wyszło Moja propozycja, ale nie wiem co dalej: http://i.imgur.com/wcT4KrR.jpg Zad.10: http://i.imgur.com/n8SVVMu.jpg Zad.11: http://i.imgur.com/qNCv1tW.jpg Zad.12 i 13: http://i.imgur.com/zvSFkch.jpg Zad.13 Nie potrafię przekształcić tej nierówności, rozbijałem −4mx na −2mx−2mx i próbowałem grupować, ale nic nie chce mi się wyłączyć Zad.14: http://i.imgur.com/9NulSpr.jpg Doszedłem do tej postaci co teraz Zad.15: http://i.imgur.com/NQtZriX.jpg Zad.16: http://i.imgur.com/QSMnkHD.jpg Zad. 17: http://i.imgur.com/FvWRyN4.jpg Rozwiązania można przybliżać sobie lupa Są dobrej rozdzielczości

pies: o ja tez to pisalem

Jack: hmm...ja bym w zad 3 dał odp c)

Jack: zad 1−5 ok (oprocz tego 3, ktore bym robil inaczej) 6 ok

Metis: 3) Z_wf=<−2,5> − zbiór wart. f(x) Zbiór wartości −3f(x)=? −f(x)= nie zmieni zbioru wartości , a jedynie monotoniczność. 3f(x) stąd <−6, 5>

Metis: *15.

Metis: Oczywiście napisałem bzdure. Zmieni. Poprawna będzie C.

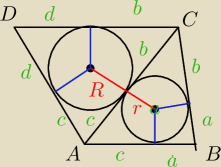
Kacper: Zadanie 7. i wszystko jasne

prosta: 3) −f(x) to symetria wykresu wzgędem Ox .... stąd przedział : <−5,2> ostatecznie: <−15,6>

Metis: Dokładnie prosta już poprawione Kacper dzięki Zerkniecie na resztę?

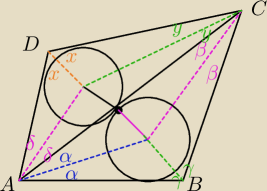
Jack: zad 7 2 (α + γ + β) = 180 α+ β + γ = 90 −−>>>γ = 90 − α − β 2(δ + x + y) = 180 δ + x + y = 90 −−>>x = 90 − y − δ 2(x + y + α + β + γ + δ) = 360 x + y + α + β + γ + δ = 180 α + δ = 180 − x − y − β − γ okrag da sie wpisac jesli 2 α + 2 δ = 2 γ + 2x czyli α + δ = γ + x = 180 180 − x − y − β − γ = γ + x 2 γ + 2x = 180 − y − β 2( 90 − α − β) + 2(90 − y − δ) = 180 − y − β 180 − 2α − 2β + 180 − 2y − 2δ = 180− y − β 360 − 2α − β − 2δ − y = 0 y + 2δ + β +2α = 360 y + β = 360 − 2δ − 2α hmm, cos chyba pochrzanilem

prosta: zad.6 dobrze zakodowane ..prawidłowe rozwiązanie powinno zawierać uzasadnienie ,że istnieje ekstremum (warunek wystarczający)... choć zastanawiam się czy przy takim sformułowaniu trzeba to liczyć.... w zadaniu kodowanym nie sprawdza się poprawności obliczeń ...(podobno) i trzeba coś zakodować...

Kacper: 9. log₄3−m=log₂(x+3) rozwiązanie ma należeć do przedziału <3,4> Zał: x>−3

1
	log23−m=log2(x+3)
2

log₂(x+3)=log₂√3−m x+3=2^{log₂√3−m} x=2^{log₂√3−m}−3 Zatem: 3≤2^{log₂√3−m}−3≤4 6≤2^{log₂√3−m}≤7

	√3
6≤		≤7
	2m

6		1		7
	≤		≤
√3		2m		√3

√3		√3
	≥2m≥
6		7

	√3		√3
log2		≥m≥log2
	6		7

	√3		√3
Odp. m∊<log2		,log2		>
	7		5

Mam nadzieję, że nie ma błędów (ciężko tu pisać)

Metis: Dzięki Kacper za chwilę przeanalizuje, a powiedz mi czy z moją próbą rozw. można coś zrobić?

prosta: zad.8

	π
dziedzina do poprawy sin2x≠1 ⇔ |sinx|≠1 ⇔ x≠		+kπ
	2

zbiór wartości: (2,+∞)

Jack: prosta, z tego co mowia nauczyciele to w kodowanych nie musi byc nic...jesli dobrze zakodujesz to masz punkty ale lepiej zawsze cos "nakreslic" czy zad 8 jest dobrze?

Metis: Dziedzina , jasne A skąd ten zbiór wartości?

Jack: 8.

	2
f(x) =
	cos2x

cos²x ∊ <0;1>

prosta: zad.8 cos²x∊(0,1) uwzględniając dziedzinę

Kacper: Zadanie 13 (takie lubię ) 8x²−4mx+2m²≥12x+6m−18 (1) Sposób I (będziemy kombinować jak "zwinąć") Wykonujemy przekształcenia równoważne: 8x²−4mx+2m²−12x−6m+18≥0 (2) (2x−m)²+(m−3)²+(2x−3)²≥0 (3) Ponieważ suma kwadratów liczb rzeczywistych jest nieujemna, to nierówność (2) jest prawdziwa dla dowolnych x i m rzeczywistych. Zatem nierówność (1) także jest prawdziwa

Jack: takie pytanie poza konkursem... Czy moge uzywac zwrotow z poza programu licealnego? bo np.nie wiem czy arc cosinus jest w programie...

Kacper: W 9 w odp błąd Ma być 6 w mianowniku.

Metis: Patrzyłem na cosx , też jasne , głupie błedy Kacper a można bez kombinowania? Kombinowałem wcześniej i nic nie wykombinowałem

Metis: Kacper skąd ta 6? Nie widzę błędu.

Kacper: Metis jak zrobię 14, to pokażę sposób "bez kombinowania"

Metis: Czekam

prosta: zad.10 dobrze

aro400: Widzę, że ja się na tej maturce nie popisałem

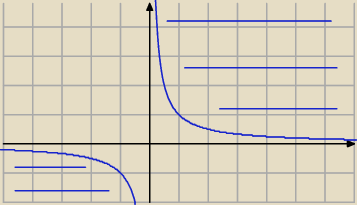
Kacper: Zadanie 14 Równanie x²−bx−2c ma dwa pierwiastki spełniające nierówność (x₁+x₂)³<x₁³+x₂³−6 1) Skoro mają być dwa, to Δ>0 Δ=b²−4*1*(−2c)=b²+8c

	b2
Δ>0 ⇔ b2+8c > 0 ⇔ c>−
	8

2) Przekształcamy (x₁+x₂)³<x₁³+x₂³−6 x₁³+3x₁²x₂+3x₁x₂²+x₂³<x₁³+x₂³−6 3x₁²x₂+3x₁x₂²<−6 x₁²x₂+x₁x₂²<−2 x₁x₂(x₁+x₂)<−2 Teraz wiemy, że x₁x₂=−2c x₁+x₂=b Zatem: −2c*b<−2 cb>1

	1
c>		, b≠0
	b

Ostatecznie mamy zaznaczyć punkty (b,c) spełniające układ nierówności:

	b2		1
c>−		i c>		, b≠0
	8		b

Rysunek powyżej

Metis: Kacper Fajne zadanko

Kacper: Zadanie 17 można zdecydowanie szybciej, ale rozwiązanie ok.

Jack: zad 15 nie wiem czy trzeba pisac, ale ja zawsze pisze ze boki > 0 wiec x,c,3x > 0

Mila: 16) A− wylosowano liczbę 3 B− suma trzech wylosowanych liczb jest nieparzysta

	4 2		5 3
|B|=5*		+		=30+10=40

	4 2		4 2
|A∩B|=		+		=12

	12		3
P(A/B)=		=
	40		10

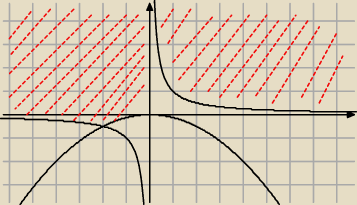
prosta: chłopaki: zad.14 cb>1 (stąd c i b są tego samego znaku ) mamy III i I ćwiartkę:

Jack: ja zazwyczaj te zadanka optymalizacyjne troszke inaczej rozpisuje, ale chyba wszystko sie zgadza i nwm czy obliczyles w koncu te najmniejsza powierzchnie czy jak... bo widze tylko wymiary no i czy usuwanie wymiernosci jest obowiazkowe to tez jest dobre pytanie

Metis: Dziękuje Milu Ogółem to zadanie jest ? Dodać jeszcze komentarze ? Jakoś mało miejsca

prosta: to okropnie podchwytliwe zadanie...zawsze tu mam wątpliwości i sprawdzam " na palcach"

Metis: Jack nie obliczyłem , ale to juz formalność Brzydkie wyniki i nie zmieściłem zapisu.

Kacper: W 16 coś za duże to prawdopodobieństwo

Metis: Mila mnie już poprawiła, prawdopodieństwo też się zmieni.

Metis: prosta powiedz o co chodzi ze sprawdzaniem na "palce"

prosta: wróćcie do zad.14 i poprawcie ....

Kacper: Zły rysunek do zadania 14 (ale każdy wie jak poprawić)

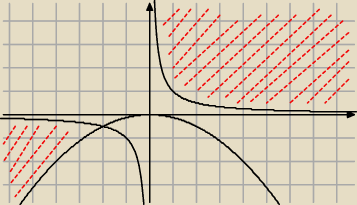
Kacper: I dlatego nie lubię komputerów

prosta: hiperbola i oś Oy dzielą płaszczyznę na 4 obszary....w każdym z nich wybieram jakiś punkt i sprawdzam, czy spełniona jest żądana nierówność. A w przedstawionym powyżej rozwiązaniu trzeba by napisać: bc>1

	1		1
(c>		i b>0) lub (c<		i b<0)
	b		b

prosta: czy u was też pdfy otwierają się z dziwną czcionką? Ostatnio tak często mi się zdarza....tutaj też przesunięcia nawiasów...i pogrubienia

Kacper: U mnie jest to samo. Możliwe, że to wina kodowania znaków.

prosta: zad. 15 spieszyłeś się strasznie....tabelka do poprawy, dopisz dziedzinę funkcji

Kacper: Muszę przyznać, że powinni was uczyć lepiej pisać w szkole

Mila: |S₁P|=R=5√2 S₂=(−3,−10), S₁=(−6,−7) |S₁S₂|=√3²+3²=3√2 r=5√2−3√2=2√2 s: y=ax+b styczna Prosta S₁S2: S₁S₂^→=[3,−3]

x+6		y+7
	=		⇔
3		−3

p: y=−x−13 Wsp. punktu P : (x+6)²+(y+7)²=50 i y=−x−13 x²+12x+36+(−x−13+7)²=50⇔2*(x²+12x+36)=50 x²+12x+36−25=0⇔x²+12x+11=0, Δ=100 x=−11 lub x=−1 i x>−3⇔x=−1 P=(−1,−12) s⊥p⇔a=1 i P∊s y=x+b, −12=−1+b, b=−11 s: y=x−11

Kacper: Dodatkowo nie widzę obliczonej powierzchni całkowitej? Straszny bałagan i może jestem ślepy?

Mila: prosta, też mam widok arkusza fatalny.

Kacper: Mila czytasz mi w myślach . Ja bym pominął liczenie promieni

Mila: Nie obliczył P_c.

Mila: Promienie nie są wykorzystane, ale na początku myślałam, że znajdę z przecięcia okręgów wsp. punktu P. Potem zmieniłam zdanie. Rysunek ( szkic) zawsze pomaga.

Metis: Dziękuje Wam za sprawdzenie Kacper post 18:21

Eta: No i nie poczekali na mnie

Metis: Eta dowód z 7 formalnie nadal nie skończony więc...

Eta: zad.7/ 1/ oznacz odpowiednio odcinki ( z tw. o odcinkach stycznych) 2/ warunek wpisania okręgu w czworokąt i masz tezę

znaffca : metis i tak napiszesz na 55 % rozszerzenie

yasumi: moglby ktos 1 rozpisaczycc wiem ze latwe ale jakos nie moge skonczyc XD

Eta:

	log90		1+2log3		2b+1
1/ log890 =		=		=
	log8		3log2		3a

Metis: znaffca niewykluczone.

Eta: Na 55% −−− to nie jest możliwe ( nie przyznają procentów nieparzystych ) A ja myślę,że na 98% ( czego Ci życzę Metis

Metis: Nie dziękuję Eta

znaffca : więc na 54 % hehehe,

Krystian : Metis − zdajesz fizykę na maturze?

Jack: ja zdaje...Metis mowil ze nie

Benny: Eta czemu nie 100%?

Krystian : Jack − z jakich podręczników / zbiorów korzystasz?

Metis: Benny , bo planimetria

Eta:

5-latek : Zebym ja miał bliżej do Ety Pozdrawiam, to pewnie udałbym się na korepetycje do niej z planimetrii

5-latek : I ciekawe czy dla przedszkolakow ma jakies zniżki

Metis: Kacper a co z tym sposobem bez kombinowania?

Eta: Dla Metiska zad.1/

	1		3
Zdarzenia A,B⊂Ω są niezależne oraz P(A\B)=		i P(B\A)=
	8		8

	7		5
Wykaż,że P(AUB)=		lub P(AUB)=
	8		8

Metis: Zrobione

Metis: http://prntscr.com/aeqd9m

Eta:

Jack: Jako ze nie mozna dodawac zadan...to dam tutaj : Uzasadnij, ze rownosc zachodzi dla dowolnej liczby x∊ℛ |log (√1+x² −x)| = |log(√1+x² +x)|

Metis: |x|=|y| ⇔ x=y v x=−y

Kacper: Metis już Musimy wykazać, że nierówność 8x²−4mx+2m²≥12x+6m−18 (*) jest spełniona przez dowolne liczby m i x. Wystarczy zatem pokazać, że nierówność kwadratowa: 8x²−(4m+12)x+2m²−6m+18≥0 jest prawdziwa dla dowolnej liczby rzeczywistej x dla dowolnej wartości parametru m. Czyli Δ≤0 dla dowolnego m. Liczymy Δ. (4m+12)²−32(2m²−6m+18)=−48 m²+288 m−432 −48 m²+288 m−432≤0 (1) (m−3)²≥0 (2) Nierówność (2) jest prawdziwa dla dowolnej wartości m. Wobec wykonanych przekształceń równoważnych stwierdzamy, że Δ≤0 dla dowolnej wartości m, zatem nierówność (*) jest spełniona przez dowolne liczby m i x. c.k.d

Krystian: Jack − z jakich podręczników / zbiorów korzystasz w przygotowaniu do matury z fizyki?

Jack: z fizyki? tylko ze szkolnych... + mamy dodatkowe kartki z roznych zbiorow na zajeciach...a tak to nic specjalnego

Jack: Kacper zerknal bys na zadanie?

Eta: Hej

5-latek : To może teraz ja Rozwiaz równanie zupełne poprzez wydzielenie pelnego kwadratu x²−5x+6=0 żeby tam było (−6x)

Jack: ma byc −6x = ... ?

5-latek : Wlasnie ze nie ma być (−5x)

Gaunt: Krystian: jeśli chodzi o fizykę to na pewno warto przejrzeć zbiór, który jest udostępniony na stronie CKE. Nie należy do łatwych, ja się dużo nad nim namęczyłam, ale na pewno wiele się można nauczyć

5-latek : Napiszse jeszcze raz to równanie dla jasności x²−5x+6=0

Jack: 5x = x² + 6 −5x = −x² − 6? ja chyba nie rozumiem co masz na mysli : D mam to rozwiazac czy jak?

	5		1
(x −		)2 − (		)2 = 0
	2		2

	6		5		1
(x −		)(x−		+		) = 0
	2		2		2

(x−3)(x−2) = 0

Mila: x²−5x+6=0⇔ x²−6x+x+6=0 (x−3)²−9+x+6=0 (x−3)²+x−3=0 (x−3)*[(x−3+1)=0 (x−3)*(x−2)=0 x=3 lub x=2

5-latek : Dobry wieczor Milu dziekuje CI bardzo Również Jack podsunal mi pomysl z wykorzystaniem (x−m)²

5-latek :

	5
czyli tak −2m=−5 to m=
	2

	5		25
wobec tego (x−		)2= x2−5x+
	2		4

wobec tego moje rownianie mogę zapisac tak

	5		1
(x−		)2−		=0
	2		4

	5		1
(x−		)2−(		)2 =0 i dalej już wiadomo
	2		2

Krystian: Gaunt − masz na myśli te 508 stron?

Kacper: Jack co masz na myśli?

Jack: post 19;43

Kacper: Po pierwsze trzeba dziedzinę wyznaczyć, a potem tak jak napisał Metis

Adrian: Miałby ktoś pomysł jak zrobić takie zadanko? Oblicz sumę pięćdziesięciu najmniejszych dodatnich liczb spełniających równanie sin4πx = 1?

Metis: Ciąg

Jack: nic to nie mowi

Adrian: Jeszcze przed odpowiedzią Metisa zacząłem z ciągiem robić i udało się rozwiązać

Adrian: a jednak nie xD, nie udało się. Pomożecie ?

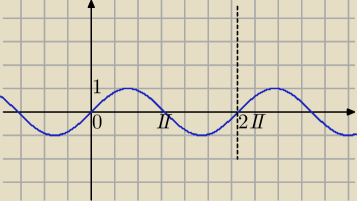
Mila: sin(4πx)=1⇔

	π
4πx=		+2kπ /:4π
	2

	1		k
x=		+		k∊{0,1,2,3,..49}
	8		2

Robert: Cześć, dalej nie można zakladac nowych tematow to zwroce tutaj do was z tym pytanim. Biore sie za powtorke planimetrii i stereometrii i czy materiały na tej stronie sa wystarczające do rozszerzenia?

Kacper: Jak przerobisz całe forum, to tak

Robert: "Całe " czyli mam rozumiec caly dzial planimeteii i stereometrii ?

Robert: Zadania mam, chodzi mi glownie o teorie, wzory twierdzenia itd