optymalizacja
rafalkoterski: Na półkuli o promieniu R opisano stozek w ten sposób, że środek podstawy stożka pokrywa
się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
12 mar 14:55
tss:
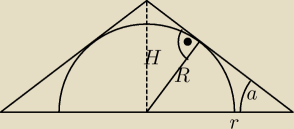
0
o<a<90
o
V=...
a
m=...
V(a
m)=...=V
min
13 mar 21:39
tss: am≈54,74o
13 mar 21:49
Eta:
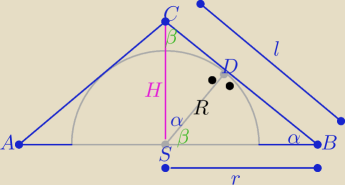
Inny sposób ( bez trygonometrii)
Z podobieństwa trójkątów SBC i SDC z cechy (kkk)
| r | | R | | r2 | | R2 | |
| = |
| ⇒ |
| = |
| i l2=H2+r2 |
| l | | H | | l2 | | h2 | |
| | H2R2 | |
to r2H2−r2R2=H2R2 ⇒ r2= |
| , H>R |
| | H2−R2 | |
V
'(H)=......................
V
'(H)=0 ................................
.................................
>>>>>>>>>>>>>>>>>>
13 mar 22:12
Laura: Pisze tutaj bo nie da sie dodac nic nowego. Dane sa dwie funkcje f(x)=x2 i g(x)=1/x oblicz
pole wyznaczane, przez te dwie funckje, uklad wspolrzednych dla x i prosta x=4
13 mar 21:10
Laura: dla x>0
13 mar 21:11
Laura: Wykres tego pola obraca sie 360 stopni wzgledem x−aksen i tworzy bryle o danej
objetosci.
Oblicz objetosc i to samo wzgledem y−aksen'
13 mar 23:35

 Inny sposób ( bez trygonometrii)
Z podobieństwa trójkątów SBC i SDC z cechy (kkk)
Inny sposób ( bez trygonometrii)
Z podobieństwa trójkątów SBC i SDC z cechy (kkk)