Trygonometria Pawel: Witajcie. Mam pytanie, jesli chce.narysowac wykres cos(2x + π) to czy najpierw rysuje Cos2x i potem przesuwam w lewo o π? Bo widzialem ze niektorzy wyciągają 2 przed nawias i troche inaczej przebiega rysowanie funkcji. Obie metody są poprawne?

Jerzy: y = − cos2x rysujesz: y = cos2x i odbijasz symetrycznie wzgledem osi OX

5-latek : Dobrze kombinujesz

Jerzy: albo: rysujesz: y = cos2x i przesuwasz o π w lewo

5-latek : Witaj Jerzy

Jerzy: Cześć

Paweł: Dziękuje bardzo za odpowiedzi, ale mam jeszcze jedno pytanie.

	π
Chce narysować wykres y = cos(2x −		)
	2

Miejsca zerowe cosinusa to π/2 + kπ. To mogę to zrobić w taki sposób?

	π		π
2x −		=		+ kπ
	2		2

2x = π+ kπ /2

	π		kπ
x =		+		Czyli to będą moje miejsca zerowe i pod k bede podstawiał liczby
	2		2

{1,2,3...} to będą moje miejsca zerowe i wtedy rysuje.

Jerzy: A po co tak kombinować ? cos(2x − π/2) = cos[−(π/2 − 2x)] = cos(π/2 − 2x) = sin2x .... i rysujeszz: y = sin2x

Paweł: Wiem, że to więcej bawienia się z tym wszystkim, ale jakoś wtedy bardziej to sobie, że tak powiem wyobrażam

Paweł: '' cos[−(π/2 − 2x)] = cos(π/2 − 2x) '' co sie stało z tym minusem ?

Jerzy: cos(−α) = cosα a co do Twojego sposobu...to popraw obliczenia

5-latek : Miałem pisać to samo

Paweł: Nie widze , gdzie się ten błąd sie wkradł ?

mietek: pytanie do 12:14 cos(2x + π) to cos2x przesuniete o π w lewo czy

	π		π
cos( 2(x +		) ) czyli cos2x przesuneite o		w lewo
	2		2

−

	π
a może cosx przesuneite o		w lewo i 2x ściśniete w poziomie?
	2

Jerzy: popatrzyłem tylko na druga linijkę .... ma być: 2x = π + kπ

	kπ
wynik masz dobry, ale można prościej: 2x = π + kπ ⇔ 2x = kπ ⇔ x =
	2

5-latek : Mietek masz programy do rysowania funkcji wiec jaki jest problem ? Ja takich niestety nie miałem i musialem wszystko rysować na papierze milimetrowym

mietek: No tak.. niby mam, ale to, że raz wyjdzie coś dobrze to nie znaczy, że reguła jest poprawna.. dlatego pytam

Paweł:

	x
Żeby niepotrzebnie nie zakładać wielu tematów . Jeśli mam taką funkcje y= 2|sin		| to
	2

jaka jest kolejność przekształceń?

Jerzy: sin(x/2) Isin(x/2)I 2Isin(x/2)I

5-latek : Korzystajac z defincji wartości bezwzlednej mamy dla x≥0

	x		1
|sin		|= sin		x
	2		2

	x		1
dla x<0 |sin		|= −sin		x
	2		2

Paweł: i jeszcze jedno. y= 2 sinx − √1−cos²x TO pod pierwiastkiem to sin²x czyli powstaje takia funkcja. y = 2sinx − |sinx| |sinx| = sinx dla sinx > 0 |sinx| = −sinx dla sinx < 0 Do narysowania mam w takim razie y=sinx dla sinx> 0 i y=3sinx dla sinx< 0, tak?

5-latek : Tak ale dla x≥0 bo sin0^o=0

Jerzy: tak

Jerzy: sinx przyjmuje wartości doatnie również dla x < 0

prosta: ale namieszaliście z tymi wykresami

prosta:

	π
a jak rysować: y= cos(2x−		) ?
	3

Paweł:

	1		1
y = sin2x * √		+		pierwiastek jest nad sumą ułamków.
	sinx		cos2x

Sprowadzam oba ułamki do wspólnego mianownika...i otrzymuje takie coś pod pierwiastkiem

	1
		Myślałem żeby teraz licznik i mianownik wymnożyć przez dwa to w mianowniku
	sin2xcos2x

otrzymam sin²2x (?) Tutaj pytanie do was czy ide dobrym tropem czy już gdzieś na tym etapie jest błąd? PS. Dzięki za poprzednie odpowiedzi

Jerzy:

	2sinxcosx
y =
	|sinxcosx|

Jerzy: poprzednie: rysujesz y = cos2x i przesuwasz o π/3 w prawo

prosta:

	π
jeśli rysujesz cos2x i przesuwasz o		w prawo to otrzymujesz:
	3

	π		2π
y=cos2(x−		)=cos(2x−		)
	3		3

Jerzy: racja

Paweł: To w takim razie jak najlepiej to zrobić?

prosta: zależy od wzoru funkcji....jeśli można zastosować wzór redukcyjny to warto....np: cos(2x−π)=cos(π−2x)=−cos2x i tylko symetria względem Ox

	π		π		π
ale ogólnie ..jak w przypadku y=cos(2x−		)=cos2(x−		) przesuwamy o		w prawo
	3		6		6

Paweł: Miałem problemy z komputerem i nie miałem jak odpisać , czyli jak rozumiem jeśli mam do

	π		π
narysowania y = cos(2x −		) to najpierw rysuje cos2x i przesuwam o		w prawo?
	3		6

prosta: dokładnie

Paweł: Dziękuje

Robert: Witajcie, jako, że nie da się utowrzyć nowego tematu na forum to się dołącze do tego jeśli

	x
można, tu trygonometria i tu. Jak będzie wyglądał wykres funkcji cos		?
	2

W ogóle to mam takie zadanie:

	x		x
Rozwiąż graficznie równanie cos		= sin
	2		2

	π		x
Skorzystałem ze wzoru i doszedłem do momentu cos(		+		) = 0
	4		2

5-latek :

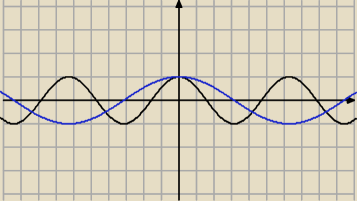
	x		1
Przeciez cos		= cos		x
	2		2

	360o
Okresem tej funkcji będzie T=		=720o
	1/2

czyli będzie to y=cos(x) ale rozciagniety 2 razy po osi OX natomiast zbor wartości tej funkcji to <−1,1>

Paweł:

	π		1
Wyznacz najmniejsze dodatnie rozwiązanie równania cos(3πx +		) +		= 0. Ktoś mógłby
	5		2

mi troszke pomóc z tym zadaniem?

	1
Myślałem		przerzucić na drugą strone, znaleźć miejsca zerowe cosinusa, narysować wykres
	2

i z wykresu odczytać, ale kiedy próbuje znaleźć miejsca zerowe to wychodzą mi jakieś brednie

Mila:

	π		1
cos(3πx+		)=−
	5		2

	π		π		π		π		π
3πx+		=		+π+2kπ lub 3πx+		=−		+π+2kπ /−
	5		3		5		3		5

	π		π		π		π
3πx=−		+		+π+2kπ lub 3πx=−		−		+π+2kπ
	5		3		5		3

	2π		8π
3πx=		+π+2kπ lub 3πx=−		+π+2kπ
	15		15

	17π		7π
3πx=		+2kπ lub 3πx=		+2kπ /:(3π)
	15		15

	17		2k		7		2k
x=		+		lub x=		+
	45		3		45		3

===========================

Paweł: a skąd w drugiej linijce wzięło sie jeszcze to jedno π?

Paweł: Ja bym to zapisał

	π		π
3πx +		= −		+ kπ gdzie leży błąd w moim rozumowaniu ?
	5		3

Paweł: ktoś coś ?

Mila:

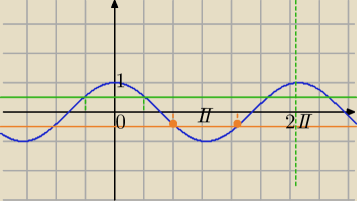
	π		1
cos(−		)=		cosinus jest funkcją parzystą
	3		2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1
cos(x)=		⇔
	2

	π		π
x=		lub x=−
	3		3

=================

	1
cos(x)=−		⇔
	2

	π		π
x=		+π lub x=−		+π
	3		3

===================== Patrz na wykres.