okrag wpisany w trójkat marianna: W trójkacie podstawa wynosi 8 oraz jego pole wynosi 12. Znajdz promień największego okregu wpisanego w ten trójkąt.

Janek191: P= 0,5*8* h = 4 h = 12 ⇒ h = 3 Mamy

	2P		24
r =		=
	L		8 + b + c

Janek191:

	4
r =		?
	3

marianna: Skąd masz ten wynik?

5-latek : A rozumiesz w ogole to co zapisal Janek191 o 10:37 ?

marianna: na tak zastosował wzór na pole P=0,5(a+b+c)r

marianna: Tylko nie wiem czemu taki rysunek

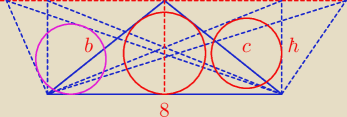
Kacper: Rysunek ma za zadanie przedstawić trochę jak wygląda sytuacja opisana w zadaniu.

marianna: No taki ale czemu tam są te pozosale okręgi, chodzi mi o jakiś sposób rozwiązania

Janek191: Masz wybrać taki trójkąt, aby promień wpisanego w niego okręgu był największy.

Janek191: Trójkątów o podstawie długości a = 8 i wysokości h = 3 jest nieskończenie wiele

marianna: Nie wiem ze ich jest nieskończenie wiele, ale jaki promień bedzie tego najwiekszego

marianna: Może akurat w trójkącie równoramiennym tak bedzie ale tego nie wiem

Janek191: Musisz to wykazać b + c jest ( ? ) najmniejsze dla Δ równoramiennego.

marianna: A jak to pokazać, w tym problem

Janek191: Właśnie

marianna: ale nie wiem czy na pewno w tym trójkacie ten promien bedzie najwiekszy

Janek191: Dla Δ równoramiennego mamy b = c = 5, więc b + c = 10 Dla Δ prostokątnego mamy b² = 8² + h² = 64 + 9 = 73 b ≈ 8,5 b + c ≈ 8,5 + 3 = 11,5 > 10 Dla Δ rozwartokątnego suma b + c jest jeszcze większa.

marianna: Czy takie rozwiązanie wystarczy?

Janek191: Tego to nie wiem. Jaki to poziom ?

marianna: liceum, rozszerzenie

Janek191: Planimetria, czy geometria analityczna ?

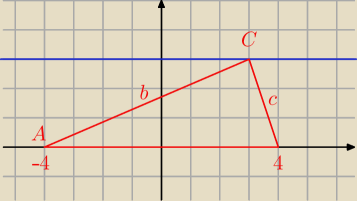
Janek191: A = ( − 4, 0) B = ( 4 , 0) C = ( x, 3) b² = ( x − (−4))² + 3² = x² + 8 x + 16 + 9 = x² + 8 x + 25 c² = ( 4 − x)² + 9 = 16 − 8 x + x² + 9 = x² − 8 x + 25 b + c = √x² + 8 x + 25 + √x² − 8 x + 25 ( b + c)(x) = f(x) = √x² + 8 x + 25 + √x² − 8 x + 25 Szukamy minimum tej funkcji:

	2 x + 8		2 x − 8
f '(x) =		+
	2√x2 + 8 x + 25		2√x2 − 8 x + 25