urna z kulami app: W urnie znajduje się 18 kul czarnych i 12 białych. Losujemy 3 kule pojedynczo za każdym razem zwracając wylosowaną. Obliczyć prawdopodobieństwo, że a) wszystkie trzy kule są czarne; b) otrzymano dokładnie dwie kule czarne. a) 18/30 * 18/30 * 18/30 b) Rozumiem, że powinno to być coś w stylu 18/30 * 18/30 * (100% prawd., że wylosowalismy kulę białą). Pytanie, czy wynikiem będzie 18/30 * 18/30 * 12/30?

kochanus_niepospolitus:

	18
a) (		)3
	30

	12*18*18
b) prawie ... wynikiem będzie 3*		... ponieważ 'kolejność' wylosowanych kul
	30

jest istotna ... a co za tym idzie −−− biała kula może być wylosowana jako pierwsza, druga bądź trzecia

Janek191: b) ? P( A) > 1 ?

matemaks: Dlaczego kolejność wylosowania kul jest istotna, skoro nie ma mowy o tym w treści zadania? Nie powinno być po prostu 18/30 * 18/30 * 12/30?

matemaks: up

matemaks:

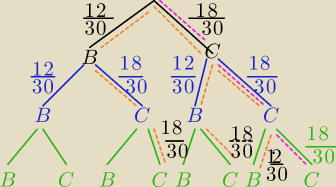
Mila: Na drzewku masz przebieg doświadczenia losowego a) A− wylosowano 3 kule czarne

	18		18		18
P(A)=		*		*
	30		30		30

b) B− wylosowano dokładnie dwie kule czarne.

	12		18		18		18		18		12
P(B)=		*		*		+		*		*		+
	30		30		30		30		30		30

	18		12		18
+		*		*		=
	30		30		30

	18		18		12
=3*		*		*		=..
	30		30		30

majka: proszę o szczegółowe rozwiązanie w urnie msamy 12 kul czerwonych i 4 białych.Losujemy 2 kule bez zwracania.Oblicz prawdopodobieństwo wylosowania 2 kul różnych kolorów

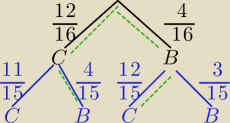
Mila: 12+4=16 − liczba kul w urnie. A −wylosowano 2 kule w różnych kolorach

	12		4		4		12		1		1		2
P(A)=		*		+		*		=		+		=
	16		15		16		15		5		5		5

majka: stokrotne dzieki