zadanie optymalizacyjne hegel: krawędź boczna ostrosłupa prawidłowego czworokątneg ma długość a,. Wyznacz taką wysokość ostrosłupa, dla której jego objętość jest największa i uzasadnij,że kąt między przeciwległymi krawędziami bocznymi jest rozwarty

Jack: Poziom studia czy liceum? bo nwm czy dwie zmienne wprowadzic i zabawa

Jack:

	1
V =		* x2 * H
	3

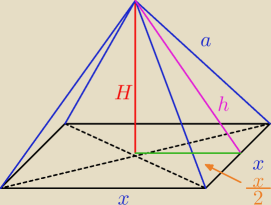
	x√2
H2 + (		)2 = a2
	2

	x2
a2 = H2 +		===>>> x2 = 2a2 − 2H2
	2

więc Objętość

	1
V=		* (2a2 − 2H2) * H
	3

	2		2
V(a,H) =		a2H −		H3
	3		3

∂V		4
	=		aH
∂a		3

∂V		2
	=		a2 − 2H2
∂H		3

	4
{		aH = 0 ==>>> aH = 0 −−−>> a= 0 lub H = 0
	3

	2
{		a2 − 2H2 = 0 ===>a2 − 3H2 = 0
	3

a² − 3H² = 0 (a−√3H)(a+√3H) = 0 a = √3H lub a = − √3H H = 0 lub H = 0 Tak naprawde mamy 1 punkt P(0,0)

∂2V		4
	=		H
∂a2		3

∂2V		4
	=		a
∂a∂H		3

∂2V		4
	=		a
∂H∂a		3

∂2V
	= − 4 H
∂H2

| 4/3H 4/3a | | | | 4/3a −4H | Podstawiamy punkt P(0,0) Wyznacznik = 0... brak ekstremow dobra skopalem tutaj cos...to sie chyba inaczej liczy

Jack: wlasciwie to post mozna usunac...

Jack: Moglby ktos inteligentny skomentowac

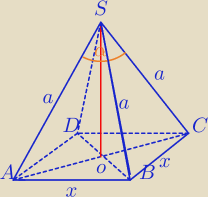Mila: x− długość boku kwadratu, x>0

	a√2
a2=H2+(		)2
	2

	x2
H2=a2−		/*2
	2

2H²=2a²−x² x²=2a²−2H², a²>H²

	1
V=		*x2*H
	3

	1
V(H)=		*(2a2−2H2)*H
	3

	2
V(H)=		*(a2*H−H3)
	3

	2
V'(H)=		*(a2−3H2)
	3

V'(H)=0⇔a²=3H²

	a2
H2=
	3

	a
H=
	√3

============

	a2
x2=2a2−2*
	3

	4
x2=		a2
	3

	8
|AC|2=x2+x2=2x2=		a2
	3

Z tw. cosinusów w Δ

	8
|AC|2=a2+a2−2*a2*cosα⇔		a2=2a2−2a2*cosα /:a2
	3

8
	=2−2cosα
3

8
	−2=−2cosα
3

2
	=−2cosα
3

	1
cosα=−		⇔α∊(90,180)
	3

hegel: Dziękuję

Jack: myslalem ze trza obliczyc...tylko tak wlasnie danych brakowalo : D