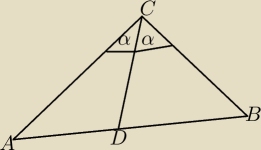
dowod planimetria planimetria: Udowodnij twierdzenie o podziale boku trójkąta dwusieczną kąta wewnętrznego: Dwusieczna kąta wewnętrznego trójkąta dzieli bok przeciwległy temu kątowi na odcinki proporcjonalne do boków przyległych, czyli (stosując oznaczenia jak na rysunku)

	|AD|		|AC|
jeżeli ∠ACD = ∠BCD , to		=
	|DB|		|CB|

W dowodzie posłuż się twierdzeniem Talesa, wcześniej jednak przedłuż odcinek AC do punktu przecięcia się z prostą równoległą do półprostej CD i przechodzącą przez punkt B.

Eta:

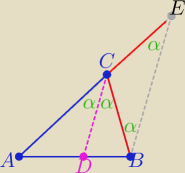
	|AD|		|AC|
Mamy wykazać ,że		=
	|DB|		|CB|

rys. jak we wskazówce .......................... ( odpowiednie komentarze do rys. trójkąt BCE jest równoramienny ( dlaczego? to: ||CB|=|CE| z tw. Talesa w trójkącie ABE :

|AD|		|AC|		|AD|		|AC|
	=		⇒		=
|DB|		|CE|		|DB|		|CB|

c.n.u