w kule wpisano stozek mat: w kule wpisano stozek o wysokosci 4. objetosc stozka jest czterokrotnie mniejsza od objetosci kuli. oblicz pole przekroju osiowego stozka odp: 16 lub 16 √√5−2

mat: ?

mat: proszee o pomoc

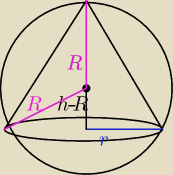
Jack: nazwijmy promien podstawy stozka jako r a promien kuli jako R h − wysokosc stozka

Jack:

	4
Vkuli =		*π*R3
	3

	1
Vstożka =		π*r2*h
	3

wysokosc stozka = h = 4 V_kuli = 4 * V_stożka

4		1
	*π*R3 = 4*		π*r2*h
3		3

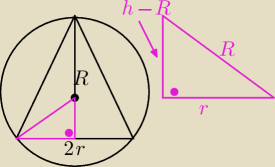
stąd R³ = r² * h R³ = 4 r² Rozpatrzmy trojkat prostokatny... z pitagorasa : R² = r² + (h−R)² R² = r² + h² − 2hR + R² h² − 2hr + R² = 0 skoro h = 4 to : 16 − 8r +R² = 0 dalej dasz rade?

Jack: aj chochlik sie wkradl... w drugim rownaniu od dolu... to jest : h² − 2hr + R² oczywiscie zamiast −2hr powinno byc −2hR czyli rownanie h² − 2hR + r² = 0 16 − 8R + r² = 0 r² − 8R + 16 = 0 skoro mamy R³ = 4r²

	R3
to r2 =
	4

podstawiajac...

R3
	− 8R + 16 = 0 /// * 4
4

R³ − 32R + 64 = 0 mozna zauwazyc ze dzieli sie przez 4 R³ − 32R + 64 = (R−4)(R² + 4R − 16) czyli mamy R = 4 albo R² + 4R − 16 = 0 stąd nam wychodza dwa z czego jeden jest ujemny i go odrzucamy, wiec drugi przypadek R = 2√5 − 2 czyli nasze R = 4 lub R = 2√5 − 2 R³ = 4r² r = ... lub r = ....

	1
Pole przekroju =		* (2r) * h
	2

mat: dzieki!