Wykaż, że najkrótszy odcinek Dawid: W kwadracie ABCD o boku długości 2 zawiera się łuk okręgu o środku w punkcie A i promieniu AB. Rozważamy wszystkie odcinki spełniające jednocześnie dwa warunki: 1) Odcinek jest styczny do danego łuku w dowolnie wybranym na tym łuku punkcie E (E≠B i E≠D). 2) Jeden koniec odcinka należy do boku BC, zaś drugi do boki DC. Wykaż, że najkrótszy odcinek spełniający warunki zadania ma długość 4(√2−1).

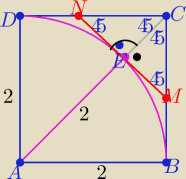
Eta: |AC|=2√2 |EC|=|AC|−|AE|=2√2−2= 2(√2−1) trójkąt MNC jest prostokątny i równoramienny to: |MN|= 2|EC|= 4(√2−1) c.n.w

Dawid: Właśnie tak zrobiłem jak trafiło się to zadanie na maturze próbnej i niestety za takie coś dostałem tylko 1 na 7 możliwych do zdobycia punktów, a teraz te zadanie w domu musimy zrobić, a mi nic innego do głowy nie przychodzi..

Kacper: Bardzo fajne zadanko, ale nie widzę rysunku Ety, a same rachunki mnie nie przekonują. Rozwiązanie przy pomocy rachunku różniczkowego dosyć proste, ale poczekajmy na rysunek Ety, bo może sie okażę, że się je w pamięci liczy, a ja będę strzelał do kaczek z "armaty" Eta można jeszcze raz rysunek?

stasius12: Dawidzie, więcej punktów nie mogles dostać, gdyż rozumowanie przedstawione przez Ete jest niekompletne − z gruntu zle założenie − bo niby dlaczego ten MN ma być taki ze DN = BM? To powinniśmy wykazać..Metoda przykładowa: Oznaczmy DN=x i BM=y .. Wówczas CN=2−x i CM =2−y. Ponadto łatwo wykazać ze DN=NE i BM=ME ( z tw. Pitagorasa dwukrotnie )... Wtedy z tw. Pitagorasa dla trójkąta NCM mamy : (2−y)² + (2−x)² = (x+y)².. Z tego równania wylivzamy jedna ze zmiennych za pomocą drugiej i liczymy sumę x+y ktora jest szukana odlegloscia wyrażoną za pomocą jednej ze zmiennych x lub y.. Czyli mamy funkcje tej zmiennej. Aby określić wartość najmniejsza liczymy pochodna i badamy ekstrema lokalne.. Itd..

Eta:

123: Jak wykazac z pitagorasa, ze DN=NE? Mógłby ktoś zapisac, bo mi nie wychodzi, ze sa rowne i nie wiem dlaczego