zadanie Metis:

	1
Udowodnij, że funkcja f(x)= 4x2+		,dla x>0 przyjmuje wartości niemniejsze od 3.
	x

Mamy zatem:

	1
4x2+		≤3 / x (x>0 wiec nie zmieni znaku nierówności)
	x

4x³−3x+1≤0 Niech g(x)=4x³−3x+1 g'(x)=12x²−3 g'(x)=0 ⇔ 12x²−3=0 , stąd

	1		1
x=		v x=−
	2		2

	1
g'(x)>0 ⇔ x∊(		,+∞) bo x>0
	2

	1
g'(x)=0 ⇔ x=		x>0
	2

	1
g'(x)<0 ⇔ x∊(0,		) x>0
	2

	1
To oznacza , że w punkcie x=		funkcja przyjmuje minimum lokalne, które jest jednocześnie
	2

jego najmniejsza wartością w przedziale (0,+∞) .

	1		1
f(		)=4*		+2=3
	2		4

Zatem funkcja f(x) dla x>0 przyjmuje wartości niemniejsze od 3. c.n. p Czy takie rozwiązanie jest w pełni poprawne? Czy brakuje komentarza, czegokolwiek?

Metis: Chyba niepotrzebnie wprowadzam nową funkcję g(x), to moze prowadzić do nieporozumień .

Godzio:

	1		1
'Funkcja maleje dla x ∊ (0,		), w x =		jest minimum lokalne, a następnie funkcja
	2		2

	1		1
rośnie dla x >		, stąd najmniejszą wartością jest f(		) = 3'
	2		2

	1
Brakuje mi tego, że f rośnie / maleje. Napisałeś tylko, że w x =		jest minimum, a nie ma
	2

uzasadnienia, że to minimum globalne (najmniejsza wartość)

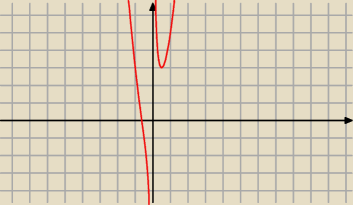
Janek191: Jest ok

Metis: Hmmm a co jeśli funkcja przyjmuje wartość najmniejszą gdzieś poza x∊(0,+∞) ? Badam i wiem, że jest to minimum lokalne w przedziale od 0 , +∞ , chyba, że coś źle rozumiem. Co do komentarza to dzięki, dodam go sobie

Godzio: Minimum lokalne − owszem, ale jak nie dodasz tego, że funkcja później rośnie, to niekoniecznie musi być to najmniejsza wartość. Nawet oczywiste rzeczy trzeba pisać

Metis: Okey, dzięki wielkie

Metis: Janek Tobie także

prosta:

	1
trzeba pisać takie rzeczy i opisywać ,że rośnie w przedziale <		,+∞)
	2

	1
a maleje w przedziale (−∞,		>
	2

a nierówność w pierwszym poście na pewno dobrze?

olekturbo: a nie powinno być ≥ 3?

prosta: powinno o tym myślał autor rozwiązania

prosta: poprawka: maleje w przedziale (0,{1}{2}>

Metis: A tak tak Źle postawiłem znak

Metis: Dzięki prosta

Jack: tak jest...na lekcji zawsze mamy obowiazkowo przedzialy monotonicznosci x ∊ .... f '(x) > 0 funkcja rosnie x ∊ ... f ' (x) < 0 funkcja maleje i stad wiemy ze zmiana znaku czyli istnieje ekstremum

Metis: Możecie mi jeszcze powiedzieć jak zapisać ten wniosek symbolicznie w stylu: http://prntscr.com/adm6gw ten zapis f(x)≥f(1)... dla mnie trochę niejasny

Mila: w x=1 funkcja ma minimum, f(1)=1 Możesz zapisać : f(x)≥1⇔f(x)>0

Metis: Dziękuje Milu

PW: Spełnione są założenia tw. o nierówności między średnią arytmetyczną a geometryczną:

	1		1		1		1		1
4x2 +		= 4x2 +		+		≥ 3(4x2·		·		)1/3 = 3√1 = 3,
	x		2x		2x		2x		2x

cbdo.

PW: Zżarło mi trójkę przed pierwiastkiem w przedostatniej równości, ale wiadomo o co idzie.

Metis: Dzięki PW, przeanalizuję.

PW: Warto, bo to zadanie "podpucha". Gdyby było sformułowane "udowodnij nierówność", raczej nie sięgalibyśmy po rachunek różniczkowy. A było "funkcja przyjmuje wartości" i automatycznie brniemy w dłuższą drogę.

PW: Popatrz też jak pięknie ICSP rozwiązał podobny problem 312959 widząc nierówność między średnimi tam gdzie inni jej nie zauważyli.

Metis: Mam nawet w zakładach W odpowiedziach jest jeszcze inne rozwiązanie, ale odrzuciłem bo ale go nie rozumiem, albo jest błędne :

	4x3−3x+1
1pkt. Zapisanie nierówności w postaci		≥0
	x

2pkt. Zapisanie nierówności w postaci x(x+1)(2x−1)²≥0

PW: Dobrze, przy założeniu x > 0

	4x2 − 3x + 1
		≥ 0
	x

to to samo co

	1
4x2 +		− 3 ≥ 0.
	x

W punkcie 2. tego iksa mogłoby nie być, jest dodatmi, więc można stronami wymnożyć przez x z mianownika zamiast myśleć w stylu "iloczyn ma taki sam znak jak iloraz".

Metis: Tylko u nich pojawiło się x³ w liczniku

PW: Tak, źle przepisałem, ale u nich jest wszystko w porządku.

Metis:

4x3−3x+1		1
	≥ 0 ⇔ 4x2+		−3≥0 gdzie x>0
x		x

Już to widzę