WORKOUT
PrzyszlyMakler: Wiem, że trochę banał, ale nie wychodzi mi wynik..
48 = a
2√3
Dobrze?
9 mar 19:59
52: a 48 to co ? Kijek od kaszanki ?
9 mar 20:01
ziomel: a czemy tej 3 nie skrociłeś xddd
9 mar 20:01
9 mar 20:02
Mila:
Do czego potrzebne a? może a2 wystarczy do dalszych obliczeń.
Napisz zadanie od początku.
9 mar 20:03
PrzyszlyMakler: Zaraz Milu napiszę, chciałem się upewnić w czymś. Czyli, taki ogólny wzór:
(a*b)12 = a12* b12 ?
9 mar 20:10
PrzyszlyMakler: Tak. Już sobie odpowiedziałem.

9 mar 20:11
52: 
9 mar 20:11
PrzyszlyMakler: Zadanie wygląda tak. Sześcian przecięto płaszczyzną przechodzącą przez przekątną dolnej
podstawy i wierzchołek górnej podstawy. Otrzymany przekrój jest trójkątem o polu 12. Pole
powierzchni całkowitej sześcianu to:
Wiemy, że 4*
4√3 = a
√2 w sześcianie
I daną, obliczoną liczbę wziąć
2 * 6 = koniec zadania?
9 mar 20:14
Mila:
W zadaniu masz dane pole przekroju 12.
Masz obliczyć Pc sześcianu?
Tak?
9 mar 20:24
PrzyszlyMakler: Tak
9 mar 20:24
Mila:
Już podaję.
9 mar 20:25
Mila:
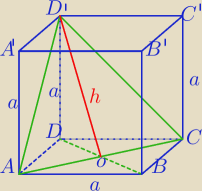
|AC|=a
√2
|AC|*h=24
a
2*
√3=24
a
2=8
√3
P
c=6a
2=6*8
√3=48
√3
==================
9 mar 20:34
Mila:
Ty liczyłeś pole z trójkąta równobocznego. Tak jest lepiej.
b=a
√2 − długość boku Δ (przekroju)
a
2√3=24
a
2=8
√3
P
c=6*8
√3
P
c=48
√3
==============
9 mar 20:44
PrzyszlyMakler: Sprytny sposób. Nie wpadłbym na to. Ja liczyłem ze wzoru na Δrównob. Dziękuję!

9 mar 20:50
Mila:
Tak właśnie trzeba było liczyć, tylko jego bok to a√2.
9 mar 20:59



