Geometria analityczna Karolina: Odcinek o końcach A(2,−3) B(6,1) jest podstawą trójkąta równoramiennego, którego jedno z ramion zawiera się w prostej x+2y−8=0. Wyznacz trzeci wierzchołek i pole trójkąta.

Tadeusz:

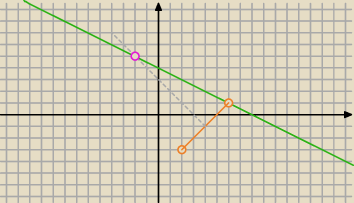
Janusz: 0) Rysunek 1)

	1+3
Znajdujemy równanie prostej AB: y =		(x−6)+ 1 = x− 5. (1)
	6−2

2) Znajdujemy współrzędne D(x_s, y_s) środka odcinka AB D ( x_s, y_s) = (4, −2) 3) Znajdujemy równanie prostej prostopadłej do prostej AB i przechodzącej przez punkt (4,−2) y = −1x +c, −2 = −1*4+c, c=2 y = −x+2 4) Znajdujemy współrzędne punktu C − przecięcia się prostych

	1
BC: y = −		x +2
	2

CD: y = −x +2 C(x_c, y_c) = (−4, 6)

	1
Pole trójkąta ABC znajdź ze wzoru na pole Δ P=		|AB|*|CD| lub ze wzoru
	2

wyznacznikowego, uwzględniając na przykład wektory AB, AC wychodzące z wierzchołka A trójkąta.

Karolina: Dziękuję