Geometria analityczna
Karolka: Na prostej y=x+4 wyznacz taki punkt C, aby trójkąt ABC był prostokątny. A(−3,1) B(3,3).
9 mar 17:28
Tadeusz:
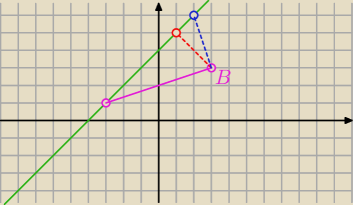
9 mar 17:40
Karolina: A można jakieś rozwiązanie?
9 mar 17:54
Tadeusz:
... nie rozumiesz czegoś ... czy czekasz na gotowca?

9 mar 17:55
Karolka: Nie rozumiem. To są dwa rozwiązania (w sensie niebieskie i czerwone)?
9 mar 17:58
Tadeusz:
dokładnie ... nigdzie nie określono przy którym wierzchołku ma być kąt prosty
9 mar 18:00
Karolka: Jedno da się obliczyć z odległości punktu od prostej a drugie?
9 mar 18:16
Tadeusz:
po co i jaka odległość punktu od prostej ?

9 mar 18:24
Karolka: To jak znaleźć te punkty?
9 mar 18:27
Janek191:
Tw. Pitagorasa.
9 mar 18:35
Janek191:
Lub proste prostopadłe do pr AB lub do pr. y = x + 4
9 mar 18:37
Milena: A mógłby ktoś rozwiązać? Nie rozumiem tego
9 mar 18:42
Janek191:
A = ( − 3, 1) B = ( 3, 3)
Prosta AB :
============
Prosta prostopadła do prostej AB przechodząca przez B:
y = − 3 x + k
3 = − 3*3 + k ⇒ k = 12
y = − 3 x + 12
==========
Szukam punktu wspólnego z prostą o równaniu y = x + 4
y = − 3 x + 12
y = x + 4
−−−−−−−−−−−−
− 3 x + 12 = x + 4
4 x = 8
x = 2
y = 2 + 4 = 6
C = ( 2, 6)
========
9 mar 20:11
Janek191:

2) Prosta prostopadła do prostej o równaniu y = x + 4 przechodząca przez B = (3,3)
y = x + 4
y = − x + m
3 = − 3 + m ⇒ m = 6
y = − x + 6
========
Szukam punktu wspólnego tych prostych:
x + 4 = − x + 6
2 x = 2
x = 1
y = 1 + 4 = 5
C
1 = ( 1, 5)
============
Zadanie ma dwa rozwiązania.
9 mar 20:18



 2) Prosta prostopadła do prostej o równaniu y = x + 4 przechodząca przez B = (3,3)
y = x + 4
y = − x + m
3 = − 3 + m ⇒ m = 6
y = − x + 6
========
Szukam punktu wspólnego tych prostych:
x + 4 = − x + 6
2 x = 2
x = 1
y = 1 + 4 = 5
C1 = ( 1, 5)
============
Zadanie ma dwa rozwiązania.
2) Prosta prostopadła do prostej o równaniu y = x + 4 przechodząca przez B = (3,3)
y = x + 4
y = − x + m
3 = − 3 + m ⇒ m = 6
y = − x + 6
========
Szukam punktu wspólnego tych prostych:
x + 4 = − x + 6
2 x = 2
x = 1
y = 1 + 4 = 5
C1 = ( 1, 5)
============
Zadanie ma dwa rozwiązania.