zadanie optymalizacyjne Natalka: Wyznacz wymiar prostokąta o maksymalnym polu którego dwa wierzchołki należna do osi OX a dwa pozostałe należą do wykresu funkcji y=4− x do potęgi 2

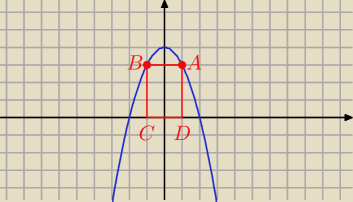
Janek191: A = ( x, y) = ( x, 4 − x² ) B = ( − x, 4 − x² ) C = ( − x, 0 ) D = ( x, 0) Pole prostokąta ABCD P = I CD I * I DA I = ( x − (−x))*( 4 − x²) = 2 x*(4 − x²) = 8 x − 2 x³ P(x) = 8 x − 2 x³

	4
P '(x) = 8 − 6 x = 0 ⇔ x =
	3

	8
I CD I = 2 x =
	3

	4		16		20
I DA I = 4 − x2 = 4 − (		)2 = 4 −		=
	3		9		9