asd
olekturbo: Jak to narysować?
Oblicz pole przekroju sześcianu o krawędzi a płaszczyzną przechodząca przez przekątne podstawy
i nachyloną do podstawy pod kątem 45 stopni.
8 mar 20:24
Gaunt:
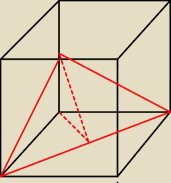
przerywane linie tworzą kąt 45
8 mar 20:28
olekturbo: Dzięki. Dla 60 stopni to będzie trapez?
8 mar 20:31
Gaunt: tak

8 mar 20:34
Gaunt: posiadaczka tej samej książki z nowej ery − pozdrawia

moje wczorajsze zadanie domowe c:
8 mar 20:35
olekturbo: | | a2 | |
dla 45 stopni wyszło mi P = |
| . Moglby ktos potwierdzic? |
| | 2 | |
8 mar 20:38
olekturbo: Również pozdrawiam
8 mar 20:38
Jack: | | 1 | | a2√2 | |
P = |
| * a√2 * a = |
| |
| | 2 | | 2 | |
hm...tak mi wyszlo
8 mar 20:41
Gaunt: A nie czasem: przekątna podstawy − a
√2
| | a√2 | |
Wysokość z trójkata 45,45: |
| *√2=a |
| | 2 | |
8 mar 20:45
olekturbo: Racja oczywiscie

8 mar 20:49
Mila:
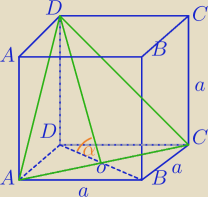
tg60
o=
√3
√2<
√3
α≈54,7
o
zatem
1) Dla α∊(o
o, 54,7
o> jest trójkątem równoramiennym
2) Dla α∊(54,7
o,90
o) przekrój jest trapezem równoramiennym,
3) Dla α=90
o jest prostokątem.
8 mar 20:51
Jack: Milu
skad brac tak dokladnie wartosci stopni?
Mam na mysli oczywiscie np. 54,7o
Z tablic mozna odczytaac ze to jest miedzy 54, a 55, a to ze to jest akurat 0,7 to jakos sie
oblicza ?
8 mar 20:56
Gaunt: Interpolacja liniowa?

8 mar 20:59
Gaunt: I przepraszam za wprowadzenie w błąd − nie doczytałam zadania, w moim bok był podany
8 mar 21:00
Mila:
W tym zadaniu wystarczy, że porównasz √2<√3 i wyciągniesz wnioski.
Wartości kąta odczytujesz w tablicach, to powinno wystarczyć.
Dawniej , gdy nie było kalkulatorów, to korzystano z tablic z tzw. poprawkami.
Na studiach poznasz funkcje cyklometryczne, wtedy nie będziesz miał tych problemów.
Ja odczytałam w wolframie
arctg(sqrt(2)).
8 mar 21:02
olekturbo: Pomoze ktos z takim samym zadaniem dla kąta 60 stopni. Nie umiem obliczyc krotszej podstawy. To
zadanie jest na forum, ale srednio mi wchodzi

8 mar 21:05
Mila:
2)
Oblicz pole przekroju sześcianu o krawędzi a płaszczyzną przechodząca przez przekątne podstawy
i nachyloną do podstawy pod kątem 60 stopni.
Tu masz rozwiązanie.
8 mar 21:13
8 mar 21:13
olekturbo: dziękuję
8 mar 21:16
Mila:
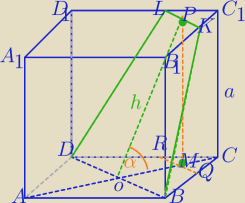
α=60
o
|PM|=a
W ΔMOP:
| | a√2 | | a√3 | | a*(3√2−2√3) | |
|MC|= |
| − |
| = |
| |
| | 2 | | 3 | | 6 | |
ΔRQC≡ΔLKC
1
ΔRQC∼ΔDBC
|RQ|=2|MC|
| | 3√2+3√2−2√3 | | √3 | |
=a2* |
| * |
| = |
| | 3 | | 3 | |
======================
8 mar 22:01
Mila:
8 mar 23:37
olekturbo: Ojej! Dzięki Milu za poświęcony czas

8 mar 23:38
olekturbo: Ten dział to dla mnie trochę czarna magia.

8 mar 23:39
Mila:
Trzeba rozwiązywać zadania, to przestanie być czarną magią.
Zobacz, może to rozwiązanie coś Ci rozjaśni problem przestrzeni.:
Dobranoc

8 mar 23:41
olekturbo: Dobranoc

8 mar 23:49
olekturbo: Zrobilem

Dzieki Milu jestes wielka! Tylko inaczej zrobilem. Wyznaczylem stosunek "k" obu
trójkatów, ale wyszło tak samo. Pozdrawiam!
9 mar 00:19
Kacper:
biorę

9 mar 20:49
olekturbo: Nauczyciel powiedział mi inny sposób. Żeby przedłużyć trapez i powstanie trójkąt. Podobno
łatwiejszy, muszę spróbować
9 mar 20:51
Kacper:
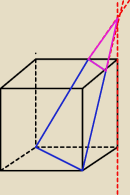
Czy ja wiem czy tak łatwiej? Jak kto woli

9 mar 20:56
 przerywane linie tworzą kąt 45
przerywane linie tworzą kąt 45

 moje wczorajsze zadanie domowe c:
moje wczorajsze zadanie domowe c:




 α=60o
|PM|=a
W ΔMOP:
α=60o
|PM|=a
W ΔMOP:




 Dzieki Milu jestes wielka! Tylko inaczej zrobilem. Wyznaczylem stosunek "k" obu
trójkatów, ale wyszło tak samo. Pozdrawiam!
Dzieki Milu jestes wielka! Tylko inaczej zrobilem. Wyznaczylem stosunek "k" obu
trójkatów, ale wyszło tak samo. Pozdrawiam!

 Czy ja wiem czy tak łatwiej? Jak kto woli
Czy ja wiem czy tak łatwiej? Jak kto woli 