Udowodnij x^2 + 2/x >= 3 gdy x >0
3nuc: Zadanie 1. (3 pkt)
| | 2 | |
Wykaż, że jeśli x > 0, to x2 + |
| >= 3 |
| | x | |
Ja robiłem tak ale mi nie wyszło:
x
3 + 2 >= 3x
x
3 − 3x >= −2
x(x
2 − 3) >= −2
x(x+
√3)(x−
√3) >= −2
i nie wiem co dalej.
Z góry dzięki za pomoc
7 mar 21:35
Jack: nic, to Ci nic nie da...
masz postać
x3 − 3x ≥ −2
wszystko na lewo
x3 − 3x + 2 ≥ 0
i teraz szukasz pierwiastkow...twierdzenie bezout znane?
albo pogrupować
x3 − 3x + 2 ≥ 0
x3 − x − 2x + 2 ≥ 0
x(x2−1)−2(x−1) ≥ 0
x(x−1)(x+1) − 2(x−1)≥0
(x−1)(x(x+1) − 2)≥ 0
(x−1)(x2 + x −2) ≥ 0
z tego drugiego delta (x2 + x − 2) <<−−z tego delta
7 mar 21:41
Kraterek: x3−3x+2≥0
Sprawdzamy, że jednym z pierwiastków wielomianu jest 1, więc dzielimy wielomian przez (x−1),
otrzymujemy funkcję kwadratową x2+x−2, którą rozkładamy z delty.
Ostatecznie po rozłożeniu (x−1)2(x+2)≥0
Pierwszy czynnik jest zawsze większy lub równy zero, bo jest podniesiony do kwadratu, a drugi
jest większy od zera, bo x jest większy od zera, a tam jest jeszcze +2.
7 mar 21:43
Jack:
po obliczeniu delty...
x
2 + x − 2 = (x−1)(x+2)
wracajac do tamtej nierownosci
(x−1)
2(x+2) ≥ 0
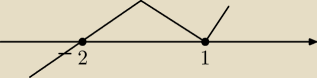
Teraz rysujemy...
(patrz rysunek)
i odczytujesz ze ta nierownosc ≥ 0 dla
x ∊ <−2;
∞)
i stad wiadomo oczywiscie ze −2 < 3
7 mar 21:45
 po obliczeniu delty...
x2 + x − 2 = (x−1)(x+2)
wracajac do tamtej nierownosci
(x−1)2(x+2) ≥ 0
Teraz rysujemy...
(patrz rysunek)
i odczytujesz ze ta nierownosc ≥ 0 dla
x ∊ <−2;∞)
i stad wiadomo oczywiscie ze −2 < 3
po obliczeniu delty...
x2 + x − 2 = (x−1)(x+2)
wracajac do tamtej nierownosci
(x−1)2(x+2) ≥ 0
Teraz rysujemy...
(patrz rysunek)
i odczytujesz ze ta nierownosc ≥ 0 dla
x ∊ <−2;∞)
i stad wiadomo oczywiscie ze −2 < 3