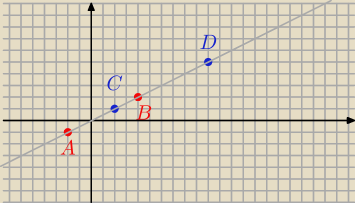
Jednokładność nie umiem matmy. :(: Sprawdź czy odcinki AB i CD są jednokładne, jeśli A( −2, −1) B(4,2) C(2,1) D( 10, 5). W przypadku odpowiedzi twierdzącej wyznacz środek S i skalę k jednokładności, w której obrazem odcinka AB jest odcinek CD. Ktoś wyjaśni jak to zrobić? Mam wyznaczyć środki odcinków AB i CD, a potem z wektorów to policzyć na zasadzie OS= k*OS₁ (nie wiem, jak tu zrobić te strzałki)?

nie umiem matmy. :(: źle napisałam. Miałam raczej na myśli SO=k*SO₁...

Janek191: Jeżeli odcinki AB i CD są równoległe, to są jednokładne.

Janek191:

	2 − (−1)		3
a1 =		=		= 0,5
	4 − (−2)		6

	5 − 1		4
a2 =		=		= 0,5
	10 − 2		8

a₁ = a₂ proste są równoległe, więc odcinki są równoległe ( jednokładne).

Janek191:

	I CD I
k =		= ...
	I AB I

Janek191:

	I CD I
k = −
	I AB I

nie umiem matmy. :(: Okej, już mniej więcej rozumiem... A punkt S?

Janek191: → → SD = k SA

nie umiem matmy. :(: Wyszło mi raczej coś źle, S(−38,−19)?

Janek191: S = (x, y) → SD = [ 10 − x, 5 − y] → SA = [ −2 − x, − 1 − x]

nie umiem matmy. :(: Skala wychodzi 4/3?

Janek191:

	4
k = −
	3