Geometria
Mała: Na zewnątrz trojkata ostrokatnego ABC zbudowano dwa kwadraty CBDE i ACFG. Punkt M jest
środkiem odcinka EF. Udowodnij ze MC=1/2AB
7 mar 20:00
Eta:
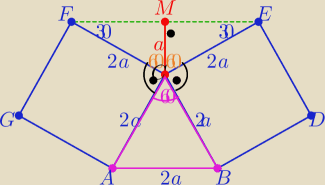
7 mar 20:30
Eta:
Rys. wyjaśnia wszystko

teraz tylko podaj odpowiednie komentarze
7 mar 20:31
Mała: Mogę założyć, że chodzi o trójkąt równoboczny?
7 mar 20:32
Eta:
Sorry...... przeczytałam "równobocznego"
7 mar 20:38
chyba nie:
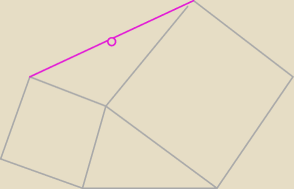
7 mar 20:42
Tadeusz:
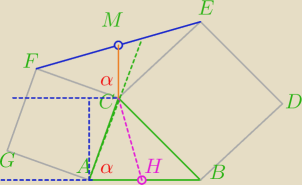
Zauważ, że pola ΔABC i ΔCEF są równe
| | 1 | |
jak również pole ΔCMF to |
| pola ΔCEF |
| | 2 | |
| | 1 | |
a pole ΔAHC to |
| pola ΔABC |
| | 2 | |
zatem pole Δ AHC równe jest polu ΔCMF
i wszystko jasne

7 mar 21:53
Mała: Dziękuje bardzo!
7 mar 22:13
Tadeusz:

7 mar 22:17
Tadeusz:
... to teraz Ty mi powiedz
Mała dlaczego pola trójkątów ABC i CEF są równe

7 mar 22:19

 teraz tylko podaj odpowiednie komentarze
teraz tylko podaj odpowiednie komentarze

 Zauważ, że pola ΔABC i ΔCEF są równe
Zauważ, że pola ΔABC i ΔCEF są równe


