Zadanie 2 Kamil: Podstawą graniastosłupa prostego jest romb o kącie ostrym 60 (stopni) . Oblicz obiętość tego graniastosłupa jeśli jego wysokość jest równa 12 cm a przekątna ściany bocznej 15 cm.

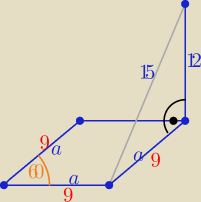
Eta: a=√15²−12²= 9 , H=12 P_p=a²*sin60^o=............. , V= P_p*H=.............

kobieta0k: a= krawędź podstawy a² + 12² = 15² a² = 15² − 12² a= √225−144 a=√81 a=9 krótsza przekątna dzieli romb na 2 trójkąty równoboczne o a=9 z zależności w trójkącie prostokątnym przekątne rombu e=9, f= 9√3 V = Pp *H Pp rombu= 1/2 e*f = 0,5* 9*9√3 V= [ 0,5* 9*9√3 *12 ] cm³ V=6*81√3 =486√3cm³

kobieta0k: małe sprostowanie: z zależności w trójkącie równobocznym, a= 9cm, 1/2 e= 4,5cm, 1/2f = 9√3 : 2 przekątne rombu e=9, f= 9√3 1

Kamil: Dzięki właśnie to ćwicze

Kamil: Mogli byście mi to wytłumaczyć, bo nie wiem skąd się wzieło a i jaki jest wzór na a= √15²−12²=9.Nie rozumiem tego.

Kamil: Czyli tam gdzie jest a² używamy wzoru na Pitagorasa tak ? a²+b²=c²

dero2005: Ściana boczna jest prostokątem o boku 12 i a. Przekątna tej ściany ma długość 15. Stąd wzór Pitagorasa a² + 12² = 15²

Kamil: A to bok c robi za przekątną d ?

Kamil: Bo przekątna 15 cm to inaczej d.

dero2005: Tak, przkątna ściany bocznej to jest przeciwprostokątna w trójkącie prostokątnym. We wzorze może być oznaczona literką c.

Eta: Co tu kombinować , podałam wszystko "na tacy"

Kamil: A chciałem się upewnić bo jutro piszę sprawdzian z stereometrii. Eta: to to co napisane to wystarczy ?

Kamil: twoje

Kamil: To ja już nie mam pytać.

Kamil: ytań*

Eta: