Wyznacz zbiór wartości parametru m dla którego równanie ma 3 różne pierwiastki Slavko: Witam Czy mógłby mnie ktoś poratować wskazówką od czego zacząć Wyznacz zbiór wartości parametru m dla którego równanie ma 3 różnepierwiastki (x−2)(x²−x)=(x−2)m

Eta: (x−2)(x²−x)−(x−2)m=0 (x−2)(x²−x−m)=0 x=2 teraz x²−x−m=0 ma mieć dwa różne pierwiastki i różne od 2 to 1/ Δ>0 i 2/ f(2)≠0 .................. dokończ

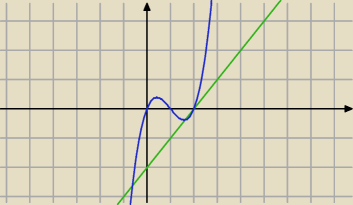
5-latek : jedynie co mi przyszlo do glowy na teraz to zrobić wykres funkcji y=(x−2)(x²−x) (niebieski i y=x−2 zielony

5-latek : Już sobie zapisuje

Slavko: (x−2)(x²−x−m)=0 Nie mogę zrozumieć skąd to się wzieło

Eta:

Eta: Wyłączamy przed nawias (x−2) z obydwu składników

Slavko: (x−2)(1−m)(x²−x) W ten sposób?

Eta: Nie! (x−2)(x²−x)−(x−2)m=0 (x−2)[(x²−x)−m]=0 (x−2(x²−x−m)=0 jasne?

Slavko: Już zakapowałem z tym czynnikiem ,przepraszam ale to moja n−ta godzina dzisiaj i końca nie widać

df: Eta, a gdyby wlasnie chciec to robic wykresem, w taki sposob, ze chcialbym doprowadzcic do postaci, ze po prawej strony mam samo m. daloby sie ? sprawdzam co sie dzieje dla x=2 , rownanie spelnione 0=0 dalej jak zakladam,ze x≠2, to mam x²−x=m , ale na tym wykresie nie odczytam 3 pierwiastkow.

df: po prawej stronie*

Slavko: Delta 1²−4*(−m) >0 1+4m >0 4m>1 m>1/4 Dlaczego f(2)≠0 ?

Slavko: Już wiem

Eta: No i gitara

df: bo moze sie zddarzyc, ze 2 bedzie pierwiastkiem tego rownania, a przeciez wszystkie maja byc rozne

Slavko: m>1/4 jest wynikiem ,tak?

Eta:

	1
Δ>0 ⇒1+4m>0 ⇒ m> −
	4

i f(2)≠0 ⇒ 4−2−m≠0 ⇒ m≠2

	1
Odp: m∊( −		, ∞) \ {2}
	4

Slavko: To dobrze mi wyszło ,dziękuje za pomoc