proszę o pomoc glax: Objętość ostrosłupa prawidłowego trójkątnego ABCS jest równa 6√3, a krawędź boczna tworzy z płaszczyzną podstawy kąt 30°. Oblicz pole powierzchni bocznej tego ostrosłupa.

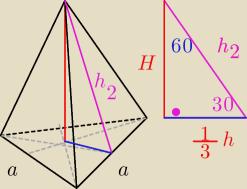
Jack: nazwijmy krawedz podstawy jako "a" z trojkata 30,60,90 wiemy ze

glax: i co dalej?

Jack:

	1		1
V =		* a2√3 *		* H
	3		4

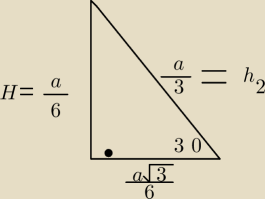
wiemy z polecenia ze V = 6√3

1
	* a2 * H = 6
12

stąd a² * H = 6 * 12 a² * H = 72

	1		a√3		a√3
1/3h podstawy =		*		=
	3		2		6

z trojkata 30,60, 90, albo z funkcji tangens, ctg, sin, cos...wiemy ze (patrz rysunek) stąd

	a		a3
a2 * H = a2 *		=		= 72
	6		6

a³ =72 * 6 = 36 * 2 * 6 = 6³ * 2 a = 6³√2 Dziwny wynik...sprawdz rachunki czy czegos nie skopalem... Pole calkowite... = P_p + P_b

	a2√3
Pp =		= ...
	4

	1		3		a		a2
Pb = 3 *		* a * h2 =		* a *		=
	2		2		3		2

glax: dziękuję