| 1 | ||
wyznacz dziedzinę funkcji f(x)= | −√X3−3x2−3x+9 | |
| x4−10x2+9 |


 War. 1. x4−10x2+9 ≠ 0
Podst. x2 = t ⇒ t2 − 10t + 9 ≠ 0
Δ=64, √Δ = 8, t1=9, t2 = 1 ⇒ x1=3, x2= −3, x3 = 1, x4 = −1
Czyli x≠3 ⋀ x≠ −3 ∧ x≠ 1 ∧ x≠ −1.
War. 2. x3 − 3x2 − 3x + 9 ≥ 0
x2(x−3) − 3(x−3) ≥ 0
(x−3)(x2 − 3) ≥ 0
(x−3)(x−√3)(x +√3) ≥ 0
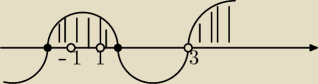
Ze złożenia warunków (na rys.) otrzymujemy dziedzinę:
D = <−√3, −1) ∪ (−1, 1) ∪ (1, √3> ∪ (3, ∞)
War. 1. x4−10x2+9 ≠ 0
Podst. x2 = t ⇒ t2 − 10t + 9 ≠ 0
Δ=64, √Δ = 8, t1=9, t2 = 1 ⇒ x1=3, x2= −3, x3 = 1, x4 = −1
Czyli x≠3 ⋀ x≠ −3 ∧ x≠ 1 ∧ x≠ −1.
War. 2. x3 − 3x2 − 3x + 9 ≥ 0
x2(x−3) − 3(x−3) ≥ 0
(x−3)(x2 − 3) ≥ 0
(x−3)(x−√3)(x +√3) ≥ 0
Ze złożenia warunków (na rys.) otrzymujemy dziedzinę:
D = <−√3, −1) ∪ (−1, 1) ∪ (1, √3> ∪ (3, ∞)