planimetria help: Dany jest trapez, na którym można opisać okrąg i w którym można wpisać okrąg. Dłuższa podstawa tego trapezu ma długość a, jedna z przekątnych ma długość ⁷₆ a . Oblicz pole tego trapezu. z góry dzięki

help: help me

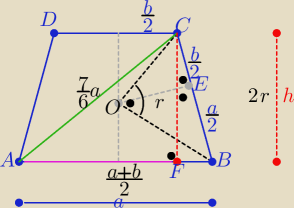
Eta: Z treści zadania ⇒ trapez jest równoramienny

	a+b
to |AB|=		i a, b >0
	2

W trójkącie BOC

	ab
r2=		⇒ 2r=√ab ⇒h=√ab
	4

z tw. Pitagorasa w ΔAFC : h²+|AF|²=|AC|²

	a2+2ab+b2		49
to: ab+		=		a2 /*36
	4		36

................................................. 40a²−54ba−9b²=0 Δ_a= 4356b² , √Δ=66b

	54b+66b		3		2
a=		=		b to b=		a
	80		2		3

h=√ab= .....

	a+b
|AF|=		=........
	2

P=|AF|*h=..........

Max Kelwin: dziękuję za pomoc nie wiem jednak skąd się wzięła równość r²=^ab₄, wyszedł mi też inny wynik niż w odpowiedziach bo tam jest ^5√6₁₈

Janek191:

	a		b		a*b
r2 =		*		=
	2		2		4

Eta: Widzę ,że nawet nie chce Ci się dokończyć prostych obliczeń ?

	a√6		5a
h = a√2/3=		i |AF|=
	3		6

to

	5a2√6
P=		[j2]] −−−− zgadza się z odpowiedzią ( gdzie zapomniałeś wpisać "a2]]
	18