dla jakich m równanie ma co najmniej 1 rozwiazanie? natka: Dla jakich wartości parametru "m" równanie lm+3l−lx−2l=m ma co najmniej jedno rozwiązanie?

natka: zagapiłam sie i pod pierwsza wartością bezwzględna powinno być x+3. B. prosze o pomoc

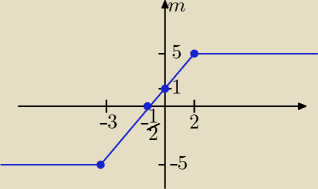
Aza: Najprościej pokazać to na wykresie rozpatrujemy wykres f(x) w przedziałach: dla x < −3 f(x) = −x −3 +x −2 = −5 dla x€<−3,2) f(x) = x +3 +x −2 = 2x +1 dla x ≥2 f(x) = x +3 −x +2= 5 dla m= −5 v m= 5 −−− równanie ma niesk . wiele rozwiązań dla m€( −5,5) −−− równanie ma jedno rozwiązanie dla m€ ( −∞, −5) U ( 5,∞) −−− równanie nie ma rozwiązania zatem odp do zad. jest równanie ma co najmniej jedno rozwiązanie gdy parametr m€ <−5,5>