stereometria hegel: czworościan foremny przecięto płaszczyzną przechodzącą przez krawędź podstawy oraz srodek przeciwległej krawędzi bocznej. Oblicz cos kąta zawartego między tą płaszczyzną a podstawą ostrosłupa

Iryt:

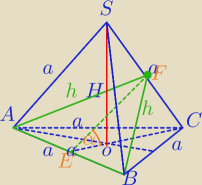
	a√3
h=|AF|=|BF|=|EC|=
	2

W ΔFEB:

	a
h2=(		)2+|EF|2
	2

	3		a2
|EF|2=		a2−
	4		4

	a2
|EF|2=
	2

W ΔFEC: |FC|²=|EF|²+|EC|²−2*|EF|*|EC|*cosα

a2		a2		3a2		a		a√3
	=		+		−2*		*		*cosα /:a2
4		2		4		√2		2

	√6
−1=−		*cosα
	2

	2
cosα=
	√6

	√6
cosα=
	3

===========

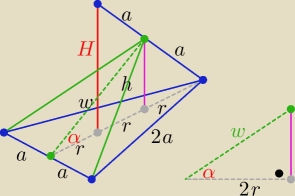Eta: Podaję inny sposób 2a −− długość każdej z krawędzi r −− dł. promienia okręgu wpisanego w podstawę 2r=R−− dł. promienia okręgu opisanego na podstawie

	2a√3
h=		=a√3
	2

	2a√3
w=√h2−a2= a√2 2r=R=
	3

	2r		2a√3		√6
cosα=		=		=
	w		3a√2		3