zad matthew: Czesc,

	1
mam takie zadanie: Kąt α jest ostry i sinα =		. Oblicz 3+tg2α.
	4

zrobilem tak:

1
	2+ cos2α = 1
4

	1
cos2α = 1 −
	16

	15
cos2α =
	16

	√15
cosα =
	4

	sinα		1     4		1		16		1
3 + (		)2 = 3 + (		)2 = 3 +		*		= 3
	cosα		√15   4		16		15		15

Może ktoś mi sprawdzić to zadanie?

Aza: ok ale można tak:

	1
sin2α=
	16

	15
cos2α=1− 116=
	16

to 3 + tg²α= 3 + ¹₁₆*¹⁶₁₅= 3 ¹₁₅

matthew: Dziekuję

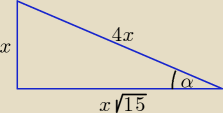
Bogdan: Albo tak:

	x		1		1		1
tgα =		=		⇒ 3 + tg2α = 3 +		= 3
	x√15		√15		15		15

matthew: Dzieki jeszcze raz Mam jeszcze takie zadanie: Rozwiąż równanie (2x+1)+(2x+4)+(2x+7)+...+(2x+28) = 155 zrobiłem tak..... a₁ = (2x+1) r = 3 obliczam a_n: a_n = (2x+1) + (n−1)*3 a_n = (2x+1) + 3n − 3 a_n = 2x +3n −2 (2x + 28) = 2x +3n −2 −3n = − 30 n = 10

	2x+1+2x+28		4x+29
155= Sn =		*10 =		*10 = (4x+29)*5 = 20x + 145
	2		2

Możecie mi sprawdzic ten przykład?

Aza: Co tu sprawdzać 4x +29= 31 => x= u{1}{2] w Twoich obliczeniach podobnie : 20x+145=155 => x = ¹₂ spr: a₁= 2*¹₂= 2 a₁₀= 1+28= 29 S₁₀= (2+29)*5= 31*5= 155

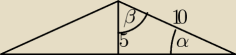
matthew: I jeszcze takie... w trojkącie rownoramiennym ABC, w ktorym |AC| = |BC| = 10cm, wysokość poprowadzona z wiercholka C jest rowna 5 cm. Oblicz miary kątó tego trojkąta. Odpowiedz podaj w kątach. zrobilem tak....

	5
sinα =		= 30o
	10

β+30^o + 90^o = 180^o β = 108^o − 120^o β = 60^o odp.: β + β = 120^o α = 30^o Może mi ktoś sprawdzić? bardzo proszę również o sprawdzenie zadania z ciągami .......

matthew: oo dziekuję

Aza:

	5		1
sinα=		=
	10		2

to miara kąta α= 30^o zatem miara kąta C = 180^o − 2*α= 180⁻ 60^o = 120^o odp: miary kątów tego trójkąta są : 30^o, 30^o , 120^o

ANNA: Dobry wieczór Aza, witaj po dłuższej przerwie.

Aza: Witaj ANNO .... za przemiłe życzenia świąteczne Sprawiłaś mi bbbb. miłą niespodziankę

matthew: zadanie z planimetrii W układzie wspolrzednych na plaszczyznie zaznaczono punkty A = (2;0) i B= (4;0). wyznacz wszystkie mozliwe polozenia punktu C, dla ktorych ABC jest trojkatem rownoramiennym o podstawie AB i polu rownym 3 zrobilem tak....

	1
P =		a * h
	2

	1
3 =		2 * h
	2

h=3 nie wiem czy dobrze to zrobilem.... możliwe są tylko dwa polozenia punktu..... Moze ktoś sprawdzić, to zadanie? Aza dzieki za poprzednie zadanie

ANNA: To cieszę się, Aza, że sprawiłam Ci przyjemność. Święta prysnęły i trzeba wracać do pracy.

matthew: ponawiam...

Aza: Ok h= 3 zatem by trójkat był równoramienny to C musi należeć do symetralnej odcinka AB zatem

	xA+xB		2+4
xC=		=		= 3
	2		2

x_C= 3 i musi być odległy od odcinka AB o 3 jednostki ( bo h= 3) zatem y_c= 3 v y_C= −3 są dwa takie punkty C spełniajace warunki zadania ( czyli dwa takie trójkąty C₁( 3,3) C₂( 3, −3)

matthew: A jak zabrac sie za takie zadanie: Wykaż, że dla m = 3 nierownosc x² + (2m − 3)x + 2m +5 >0 jest spelniona przez wszystkie liczby rzeczywiste x. Δ = (2m −3)² − 4 * (2m+5) = 4m² −12m +9 − 8m − 20 = 4m² −20m −11 1) dla m=3

Aza: No prosto podstawiasz za m= 3 x² +3x +11 > 0 Δ =9−44<0 −−−brak miejsc zerowych i ramiona paraboli do gory więc rozwiazanie nierówności jest x€ R

matthew: kurcze.... tez tak kombinowalem, ale jak zobaczylem jaka mi delta wyszla, to sie przerazilwem.... w sumie to nie wiedzialem o co tak dokladnie chodzi w tym zadaniu Dzieki za odpowiedz

Aza:

matthew: mam jeszcze takie zadanie: Jednym z miejsc zerowych funkcji kwadr. f jest liczba 5, maksymalny przedzial, w którym ta funkcja jest malejąca to <2, +∞). Najwieksza wartosc funkcji f w przedziale <−8; −7> jest rowna (−24). Wyznacz wzor funkcji f i narysuj jej wykres. I tak wywnioskowałem, że funkcja ma m. zerowe x₁ = 5 i x₂ = −1 ponieważ napisane jest, że funkcja jest malejąca w przedziale <2, +∞) wiec wierzcholek paraboli znajduje sie w miejscu 2 na osi x, nie wiem na jakim poziomie przy osi y. nie wiem jak dalej........

Godzio: największą wartość przyjmuje w przedziale w którym funkcja jest rosnąca więc f(−7) = −24 podstaw ten punkt do postaci iloczynowej oblicz "a" i wymnóż i masz wzór

Aza: ok teraz postać iloczynowa f(x) = a ( x −5)( x+1) a <0 oraz przedział <−8, −7> jest na lewo od x_w= 2 więc f( −7) = −24 podstawiając otrzymasz: −24= a( −7 −5)( −7+1) ....... wyznacz wartość "a" i podasz f(x) ....... powodzenia

matthew: nie jestem pewien..... −24 = a(−7−5)(−7+1) 72a = −24

	−24		1
a =		=
	72		3

	1
y =		(x−5)(x+1)
	3

	1
y =		(x2 +x −5x −5)
	3

	1		4		5
y = −		x2 +		x+
	3		3		3

matthew: Dzieki za odpowiedzi

Aza:

	1
a= −
	3