Punkt należy do odcinka stokrotkę: Punkt P należy do odcinka o końcach A(−20,20) i B(60,60). Jeśli 4|BP|=|AB|, to punkt P ma współrzędne: Długość AB mi wyszła √8000... Pomoże ktoś?

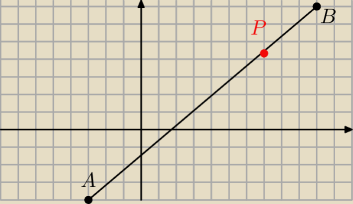
5-latek : To jest taki szkic do zadania żeby wiedzieć o co chodzi

Janek191: P = (x, y) → → AB = 4 PB

Janek191: → AB = [ 60 − (−20), 60 − 20 ] = [ 80, 40 ] → PB = [ 60 − x, 60 − y ] więc [ 80, 40 ] = 4*[ 60 − x, 60 − y ] = [ 240 − 4 x; 240 − 4 y] 80 = 240 − 4 x 40 = 240 − 4 y 4 x = 160 4 y = 280 x = 40 y = 70 P = ( 40, 70 ) ==========

Jack: Kontynuujac post Janka 15;07 → AB = [80, 40] → PB = [60−x , 60 − y] [80, 40] = 4 [60−x , 60 − y] [80,40] = [240 − 4x, 240 − 4y] {240 − 4x = 80 {240 − 4y = 40 stąd 4x = 160 −>>> x = 40 4y = 200 −>>> y = 50 P(40, 50)

5-latek : Punkt P będzie miał wspolrzedne

	x1+k*x2
x=
	1+k

	y1+k*y2
y=
	1+k

gdzie k to stosunek podzialu dawniej takich wzorow wlasnie uzywalem . Zastanow się w jakim stosunku punkt P dzieli odcinek AB ?

Jack: Janek oczywiscie ma malego chochlika, punkt P lezy pomiedzy A i B wiec nie moze miec wspolrzednej igrekowej wiekszej jak 60

Janek191: Pomyłka: 40 = 240 − 4y 4 y = 200 y = 50 P = ( 40, 50 ) ===========

5-latek : Jeśli zauważysz ze punkt P dzieli odcinek AB w stosunku k=3:1 to

	−20+3*60
x=		= 40
	1+3

	20+3*60
y=		= 50
	1+3

Eta: dla 5−latka

5-latek : Dzien dobry Eta dziekuje za

Jack:

Eta: k=3

	xA+k*xB
xP=
	1+k

	yA+k*yB
yP=
	1+k

Eta: Analogicznie k=1

	xA+1*xB		xA+xB
zatem: xS=		=
	1+1		2

	yA+yB
yS= .......................... =
	2

S−− jest środkiem odcinka AB

5-latek : I mamy wyprowadzone wzory na srodek odcinka czyli już wiemy nie tylko jakie sa ale dlaczego sa takie . Pieknie Eta