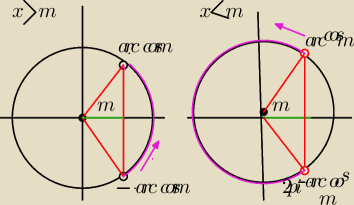
Kolo trygonometryczne 5-latek : Witam . Rozpatrujemy elementarne nierownosci cosx>m i cosx<m jeśli m<−1 to nierownosc cosx>m jest spelniona natomiast nierownosc cosx<m jest sprzeczna Tak samo jeśli m>1 to nierownosc cosx>m jest sprzeczna a nierownosc cosx<m jest spelniona Teraz jeśli −1≤m≤1 to nierownosc cosx>m jest spelniona w przedziale −arccosm<x<arccosm Natomiast nierownosc cosx<m jest spelniona w przedziale arccosm<x<2π−arccosm teraz narysujemy to na kole trygonometrycznym dla m >0 Dlaczego jest dla cosx<m 2pi−arccosm ? jakie będą oznaczenia na kole trygonometrycznym jeśli m<0 ?

5-latek : Oczywiście wtedy m będzie na lewo bo ta zielona linia to linia cosinusa Zadaja aby wykonać odpowiednie rysunki

5-latek : Chce to najpierw rozpatrzyć na kole trygonometrycznym a potem dopiero na wykresie y=cosx

5-latek :

iryt: Witaj. Porzuć koło. Rozważaj wykres.

5-latek : Dzieki zaraz się za to wezme

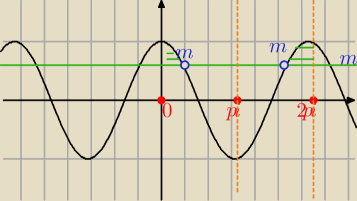
5-latek : mam wykres y=cos(x) rozpatruje okres <0,2π> mamy tutaj rozwiązanie rozwania cosx=m>0 x=arc cos m₁ i x=−arc cosm mamy rozwiazac nierownosc cosx>m Wiec tak na tym przedziale będzie Nie wiem jak to zapisac natomiast dla cosx<m x∊(arccosm ,2π−arcosm) Potem się zajme dla m<0

5-latek : tak mysle Iryt nad tym zapisem dla cosx>m i przychodzi mi tylko do glowy taki x∊(arccosm ) U(2π−arccosm ,2π) ale czy dobry ? Jak to zapisac dla m=0,5 np. ?

Iryt: W przedziale <−π,π> Dla −1≤m<1 −arccos(m)+2kπ<x<arccos(m)+2kπ

5-latek : [\Mam Iryt narysowany to dla m>0 w przedziale taki jaki podalas . Chcialem to zrobić w innym natomiast w przedziale <−π,π> cosx>m to rozwiązanie szcegolne −arccos(m)<x<arccos(m) natomiast ogolne będzie 2kπ−arccos(m)<x<arccos(m)+2kπ

Iryt:

5-latek : na razie zostawiam te nierownosci na później . Teraz zajme się wzorami na sume i roznice , polowkowymi Potem zajme się rownanianimi . Chociaz to kolo jest ciekawe