Wykaż że prawidłowe są równości:
Kadziu: Jak to rozwiązać?
| | √6+√2 | |
a) √3+√5−√13+√48= |
| |
| | 2 | |
Jedynie wpadłem na pomysł że:
ale dalej nie mam pomysłu
| | √5−2√6*(5+2√6)*(49−20√6) | |
b) |
| |
| | √27−3√18+3√12−√8 | |
Podobnie tylko doszedlem do wniosku że:
| √5−2√6*(5+2√6)*(49−20√6) | |
| |
| (√3−√2)3 | |
5 mar 13:34
Jack: a) sprzeczne, to jest bledne...
chyba ze zle przepisales
5 mar 13:37
Jack: b) to sie czemus rowna, czy masz przeksztalcic do najprostszej postaci...czy jak? ;
5 mar 13:38
Kadziu: co do podpunktu a − przepisalem dobrze , kropka w kropke.
a w b − zapomnialem dopisac że ma sie to wszystko równać 1.
5 mar 13:40
Jack: a) no to trudno, ale jest falszywe...
5 mar 13:41
Jack: b)
Mozesz zauwazyc, ze
√5−2√6 = √3−√2
(5+2√6) = (√3+√2)2
5 mar 13:44
Jack: oraz
49 − 20√6 = (5 − 2√6)2
5 mar 13:45
Jack: b) jak podstawisz to wszystko...
to masz:
| (√3−√2)*(√3+√2)2*(5−2√6) | |
| = |
| (√3−√2)3 | |
| | (√3+√2)2*(5−2√6) | |
= |
| = |
| | (√3−√2)2 | |
Zauważ, że
| (√3+√2)2 | | (√3+√2)2 | |
| = |
| , a po usunieciu niewymiernosci : |
| (√3−√2)2 | | 5−2√6 | |
= (
√3+
√2)
2 * (5+2
√6) = (5+2
√6) * (5+2
√6) = (5+2
√6)
2 = 49 + 20
√6
czyli wlasciwie nie musielismy tamtego zamieniac...
to ostatecznie mamy
(49 + 20
√6)(49 − 20
√6) =2401 − 2400 = 1
5 mar 14:08
Krzysiek: Jack, a) jest prawdziwe
5 mar 14:12
Jack: oczywiscie ze nie
5 mar 14:30
Krzysiek:
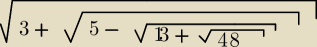
| | √6+√2 | |
Autorowi chodziło o takie działanie, a to już jest równe |
| |
| | 2 | |
5 mar 14:41
Jack:

Hmm...bylem pewien ze tak...
5 mar 14:45
5-latek : Ja tez jak Jack
Ale Kadziu na to gdzies i ja tez
5 mar 14:47
Kadziu: Hmm ... tak , chodziło mi tak jak krzysiek to narysował.
Tak wogole nie wiedziałem że podpunkt b jest taki łatwy xd
5 mar 14:50
Jack: jak takie proste to b) zrob sam, na tym samym polega
5 mar 15:00
Krzysiek: W a) wystarczy parę razy podnieść do kwadratu obie strony... Na końcu wyjdzie, że √48 = 4√3
5 mar 15:05
Jack: b)
jesli mowisz ze zapis Krzyśka z postu o 14;41 jest poprawny, to
√48 = 4
√3
teraz
√ 13 + 4√3 =
√(1+2√3)2 = 1 + 2
√3
dalej idąc mamy
√5 − (1+2√3) =
√4 − 2√3 =
√(√3−1)2 =
√3 −1
Dalej mamy :
√3 + √3−1 =
√2 + √3
| | 1 | |
Teraz wystarczy wykazac, ze √2 + √3 = |
| (√6+√2) |
| | 2 | |
a zatem
| | 4+2√3 | | √3+1 | | √2(√3+1) | | √6+√2 | |
√2 + √3 = √( |
| ) = |
| = |
| = |
| |
| | 2 | | √2 | | 2 | | 2 | |
5 mar 15:08
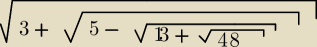
 Hmm...bylem pewien ze tak...
Hmm...bylem pewien ze tak...