Wart. Bezwgledna Paweł: Witajcie, potrzebuje pomocy przy tej.nierówności którą chce rozwiązać. |x²−2x|≥x³ mam to rozpatrYc na dwa przypadki? I w zależności od tego zmieniac znak przed wartością bezwzgledna? Prosze o pomoc i z góry dzięki za każdą rade?

guug: x(x−2) rysujesz oś i sprawdzasz kiedy ≥0, a kiedy <0

Jack: 2 przypadki : 1) x² − 2x ≥ 0 2) x² −2x < 0

Jerzy: 1) założenie: x³ ≥ 0 2) .. ⇔ x² − 2x ≥ x³ lub x² − 2x ≤ − x³

Jerzy: Podstawą w tym zadaniu jes założenie,że prawa strona musi być nieujemna

Jerzy: wycofuję ostatni wpis i założenie 1) ... źle popatrzyłem

Paweł: Czyli to co napisal Jack jest dobre?

Jerzy: Tak

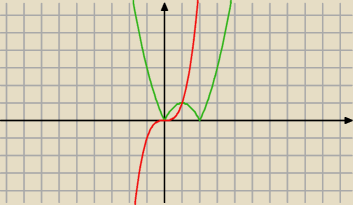
Jerzy: I rozwiązanie graficzne

PW: Nierówność |x² − 2x| ≥ x³ jest spełniona w sposób oczywisty dla x ≤ 0 (bo prawa strona niedodatnia, a lewa nieujemna). Część rozwiązania już mamy: wszystkie liczby z przedziału (−∞, 0>. Dla pozostałych x, to znaczy dla x∊(0,+∞) |x|·|x − 2| ≥ x³ obie strony można podzielić przez dodatnie x = |x| uzyskując równoważną nierówność |x − 2| ≥ x², x∊(0,+∞), którą osobno rozwiązujemy na przedziale (0,2) i osobno na przedziale <2,∞).

Paweł: I jak rozpatrzr te dwa przypadki yo.jak wpleść te x³?

Paweł: O kircze. Nie wczytalo mi dwoch ostatnich odpowiedzi. Juz je czytam

Krzysiek: ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++