trapez ostrosłup mat: Podstaw ˛a ostrosłupa ABCDS jest trapez równoramienny ABCD, którego ramiona mają długość |AD| = |BC| = 16√2 i tworzą z podstaw ˛a AB kąt ostry o mierze 45◦ Kazda ściana ˙ boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym k ˛atem α takim, ze tg ˙ α = 15/8 . Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej SAD.

mat: pomoże ktoś ?

mat: nikt nie umie ?

Eta: Większość "umie" Rys. wykonałeś?

mat: Tak wykonałem. Doszedłem do wniosku, że skoro tangens jest taki sam, to spodkiem wysokości musi być środek okręgu opisanego na tym trapezie. I tyle mam na razie, nie wiem co dalej

mat: No i mam jeszcze wysokość tego trapezu w podstawie wynosi ona 16.

mat: skoro większość umie to może ktoś pomoże

Eta: I tu się mylisz Jeżeli wszystkie ściany ostrosłupa są nachylone pod tym samym kątem do podstawy to spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu wpisanego w podstawę

mat: tak racja oczywiści o to mi chodziło, źle tu na forum napisałem Co nie zmienia faktu, że nie wiem jak dalej to liczyć. Wysokość trapezu = 2r

mat: @Eta czy wysokość trapezu = średnica okręgu wpisanego w ten trapez

mat: 120/17 ?

Eta: h=2r=16 ⇒ r=8=|OE| Wytnij trójkąt prostokątny z rys. w ostrosłupie 8k=8 ⇒ k=1 to H= 15 to h_b= .....

	1		1
P(ΔOES)=		H*|OE| i P(ΔOES|=		*d*hb
	2		2

z równości pól wyznaczysz szukaną odległość "d" Powodzenia Idę ,bo mi się szarlotka spali

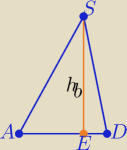
Eta: Podaję 2 rys. ( ściana ADS) dla jasności