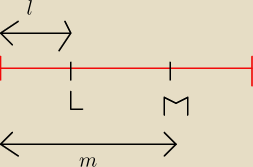
prawdopodobieństwo geometryczne Bambuko: Na odcinku [0,1] umieszczono losowo punkty L i M. Jakie jest prawdopodobieństwo, że środek odcinka LM należy do [0, 1/3]? Nie mogę za chol.... zrozumieć dlaczego zapis warunku zdarzenia A wygląda następująco: (x+y)/2 ≤1/3 zamiast |x−y|/2≤1/3 Przecież żeby obliczyyć środek długości odcinka muszę wziąć moduł i z ich różnicy, bo nie wiem który jest dłuższczy a który krótszy, liczyc odległość zaczynam również od 0.

Bambuko: zamiast l i m(małe literki) ma być x i y

Janek191: Środek odcinka

x + y
2

Bambuko: ale przecież to są odległości mierzone od początku układu czyli od 0

aight: but nigga i'm 3hunna

Janek191: 0 < x < y to

y − x
	− długość połowy odcinka o końcach x , y.
2

Bambuko: Ok już rozumiem, dzięki

jc: Narysuj kwadrat [0,1]x[0,1]. Każdy punkt w kwadracie to para punktów na odcinku: (x,y). Interesują nas punkty, dla których (x+y)/2 ≤ 1/3, czyli x+y ≤ 2/3. Punkty te leżą w trójkącie o wierzchołkach (0,0), (0,2/3), (2/3,0). Szukane prawdopodobienstwo = Pole Δ / Pole □ = 2/9