qwerty
lenovo: Zaznacz w układzie współrzędnych wszystkie punkty, których współrzędne (x,y) spełniają
nierówność x+|x|≥y+3*|y|. Wiem że będe miał 4 przypadki. W pierwszym przypadku zapisałem swoją
nierówność tak: x+x≥(y+3)y. Żeby mieć równanie prostej to muszę przerzucić y na lewą stronę a
x na prawą prawda? Jakby ktoś mógł rozwiązać tą nierówność po kolei byłbym bardzo wdzięczny
Mila:
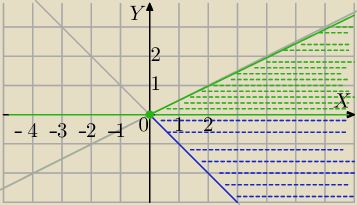
x+|x|≥y+3*|y|
1) y≥0 wtedy mamy nierówność :
x+|x|≥y+3y⇔
4y≤x+|x| /:4
a) x≥0 i y≥0 ( I ćwiartka)
| | 1 | | 1 | |
y≤ |
| *(x+x)⇔y≤ |
| x punkty w I ćwiartce pod wykresem y=2x i na półprostej |
| | 4 | | 2 | |
b) x<0 i y≥0
x−x≥4y ( II ćwiartka)
y≤0 punkty na ujemnej półosi OX
2) y<0 (III i IV ćwiartka)
a)
x≥0 i y<0
x+x≥y+3*(−y)
2x≥−2y /:(−2)
−x≤y punkty w IV ćwiartce powyżej prostej y= −x i na półprostej
b)
x<0 i y<0
x−x≥y−3y
0≥−2y
y≥0 brak rozwiązań.