W parku znajduje się klomb w kształcie trójkąta równobocznego sienko10: W parku znajduje się klomb w kształcie trójkąta równobocznego z trzema sadzawkami sty cznymi do siebie i do brzegów klombu. Wyznacz stosunek powierzchni sadzawek do powierzchni całego klombu. Podaj wynik w procentach zaokrąglony do liczby całkowitej. Rysunek: http://pl.static.z-dn.net/files/dd6/e3cd022258b756fab4f7e7c03e4dd949.png

Tadeusz: podpowiedź: Wyznacz bok za pomocą promienia

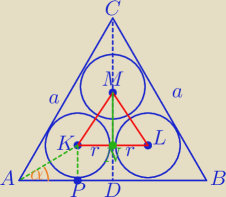
Mila: |ΔKLM− Δrównoboczny o boku 2r W ΔAPK: α=30^o

	r
tgα=
	AP

	r
tg(30o)=
	AP

√3		r
	=
3		AP

	3r
|AP|=
	√3

	a
|AP|=r√3 i |AP|=		−r⇔
	2

a
	−r=r√3
2

a
	=r√3+r
2

	a
r*(√3+1)=		/*(√3−1)
	2

	a
r*(3−1)=		*(√3−1) /:2
	2

	a
r=		*(√3−1)
	4

	a
Po=π*(		*(√3−1))2
	4

	a2
Ps=3*		*(4−2√3)
	16

	3a2
Ps=		*(2−√3)
	8

	a2√3
PΔABC=
	4

Ps		3a2		4		√3*(2−√3)
	=		*(2−√3)*		=
PΔ		8		a2√3		2

Posprawdzaj rachunki.

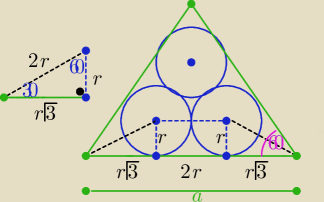Eta: a=2r+2r√3 = 2r(√3+1) to a²= 4r²(4+2√3 =8r²(2+√3

	a2√3
PΔ=		⇒ PΔ= 2r2(2√3+3}) , Ps= 3πr2
	4

Ps		3π
	=
PΔ		2(2√3+3)

Można jeszcze usunąć niewymierność z mianownika