Ciągi i wykres funkcji M.C: Witam mam problem z 2 zadaniami z matury rozszerzonej i nie wiem jak to zrobić Nawet mała podpowiedź mi pomoże 1. Ciąq (a_n) o wyrazach dodatnik jest określony wzorem rekurencyjnym a₁ = 3 log₃a_n+1 =log₃a_n +1 dla n>=1

	log3an+1
udowodnij: lim n−> nieskończoności		=1
	log3an

2. wyznacz wszystkie punkty o całkowitych współrzędnych leżące na wykresie funkcji

	2x+1
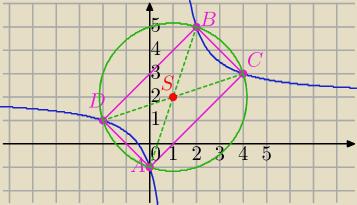
f(x) =		. Napisz równanie okręgu przechodzącego przez te punkty
	x−1

Janek191:

	2*( x − 1) + 3		3
2) f(x) =		= 2 +		; x ≠ 1
	x − 1		x − 1

Mila: 2) x≠1

	2x−2+2+1		2*(x−1)+3		3
f(x)=		=		=2+
	x−1		x−1		x−1

	3
wyrażenie		ma wartość całkowitą dla :
	x−1

a) x−1=−1⇔x=0 f(0)=2+(−3)=−1 A=(0,−1) b) x−1=1 ⇔x=2

	3
f(2)=2+		=5
	1

B=(2,5) c)x−1=3⇔x=4 f(4)=2+1=3 C=(4,3) d) x−1=−3⇔x=−2 f(−2)=2+(−1)=1 D=(−2,1) AD^→=[−2,2] AC^→=[4,4] AD^→ o AC^→=−8+8=0 wektory są prostopadłe W czworokącie ACBD przeciwległe boki są równe⇔czworokąt jest równoległobokiem. Jeden kąt jest prosty, to pozostałe również . środek okręgu opisanego na prostokącie leży na przecięciu przekątnych. S− środek AB, A=(0,−1),B=(2,5)

	0+2		−1+5
S=		,		)=(1,2)
	2		2

R=|AS|=√1²+(2+1)²=√10 równanie okręgu: (x−1)²+(y−2)²=10

5-latek : Witam Milu Pozdrawiam

Mila: Witaj

M.C: Dzieki Mila zanim napisałaś doszedłem do policzenia 4 wierzchołków chodź nie wiedziałem jak udowodnić czy to jest prostokąt i jak policzyć R a czy wiesz jak policzyć 1?

Mila: 1) a₁=3 log₃(a₂)=log₃(a₁)+1 log₃(a₂)=log₃(3)+log₃(3) log₃a₂)=log__3(3*3) a₂=9 log₃(a₃)=log₃(a₂)+1 log₃(a₃)=log₃(9)+log₃(3) log₃(a₃)=log₃(27) a₃=27 3,9,27,.. c.g a₁=3 , q=3 a_n=3*3ⁿ⁻¹=3ⁿ a_n+1=3ⁿ⁺¹

	log3(an+1)
lim n→∞		=
	log3(an)

	log3(3n+1)
=lim n→∞		=
	log3(3n)

	(n+1)*log3(3)		n+1
=lim n→∞		=lim n→∞		=1
	n*log3(3)		n