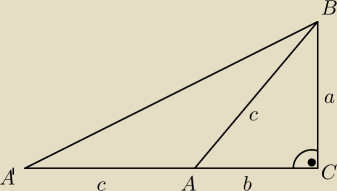
W trójkącie Tr: W trójkącie prostokątnym ABC przedłużono bok AC poza punkt A o długość C, oznaczając koniec przedłużenia A' 1) Udowodnij, że kąt AA'B jest połową kąta CAB 2) Wykorzystując punkt pierwszy udowodnij, że

	α		a
tg		=
	2		b+c

Wykorzystując punkt drugi:

	α		5
3) Oblicz tg		jeśli tgα=
	2		12

4) Oblicz dokładne wartości tg15 i tg22,5

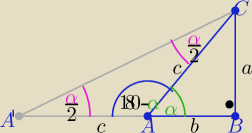Eta: 1/ trójkąt AA^'C jest równoramienny o ramionach długości "c"

	α		α		α
to |∡AA'C|= |∡ACA'|=		to |∡BAC|=		+		= α
	2		2		2

c.n.u

	α		|BC|		a
2/ w trójkącie BA'C : tg		=		=
	2		|AB|+|AA'|		b+c

	5
3/ jeśli tgα=		to a=|BC|=5k i b=|AB|=12k , k>0 ⇒ c= |AC|=√25k2+144k2= 13k
	12

to

	α		a		5k		1
tg		=		=		=
	2		b+c		12k+13k		5

Eta: 4/ dla α=30^o

	α		a		a		1
tg		= tg15o=		=		=		= ....=2−√3
	2		b+c		2a+a√3		2+√3

dla α=45^o

	α		a		a		1
tg		= tg22,5o=		=		=		= √2−1
	2		b+c		a+a√2		√2+1

Tr: Dzięki

Eta: