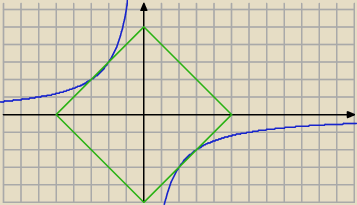
Oblicz współrzędne punktów przecięcia się figur określonych równaniami Pytak: Oblicz współrzędne punktów przecięcia się figur określonych równaniami |x| + |y| = 5 i xy = −6 Doszedłem do wniosku, że będą 4 przypadki y = 5 − x y = 5 + x y = −5 + x y = −5 − x Przekształciłem powyższe w ten sposób aby zawsze można było podstawić pod xy = −6 Podstawiając powyższe przypadki pod równanie xy = −6 zawsze wychodzi równanie kwadratowe. x(5 − x) = −6 | x1 = −1 | x2 = 6 x(5 + x) = −6 | x1 = −3 | x2 = −2 x(−5−x) = −6 | x1 = −6 | x2 = −1 x(−5−x) = −6 | x1 = −6 | x2 = 1 I zacząłem się gubić. proszę o wytłumaczenie przykładu i wskazanie błędów.

Qulka: rozpatrz w kolejnych ćwiartkach a tak naprawdę tylko w dwóch w których jest hiperbola

olekturbo: |x| + |y| = 5 to kwadrat o środku (0,0) i boku = 5.

	−6
a z drugiego y =
	x

najlepiej narysowac

Qulka:

Qulka: jak dla mnie to ten kwadrat ma bok 5√2