#workout 11 PrzyszlyMakler: Miejscami zerowymi tej funkcji są liczby −2 i 1. Oblicz współczynnik kierunkowy trójmianu ax² +3x −6. Nie wiem jak to ugryźć.

PrzyszlyMakler: Dobra. Zrobiłem. Banał i udawajcie, że nigdy tego nie napisałem.

PrzyszlyMakler: Bardzo szybkie pytanie. Czy jeżeli mam układ: w² = 100 − y² to mogę zapisać w= 10 − y

Metis: Nie.

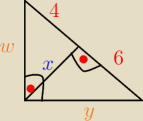
PrzyszlyMakler: Mam takie zadanie. Sądzę, że rysunek jest dość czytelny. Mam wyznaczyć x. Czerwone kropki to kąty proste. Oznaczyłem sobie w i y jako przyprostokątne i doszedłem do takich przekształceń. 6² + x² = y² 4² + x² = w² w² + y² = 10² To jest dobry trop? By mi coś z tego wyszło? Na pewno musi być łatwiejszy sposób, bo to zadanie z podstawy za 1pkt..

Metis: x=√4*6... tyle.

PrzyszlyMakler: Z jakiej racji? Błagam o wytłumaczenie! XD

Metis: Znana własność, którą wypadałoby pamiętać. 46522

PrzyszlyMakler: Nie mam pojęcia z czego to wynika, ale dziękuję.

Metis: Przecież masz tam napisane. Z podobieństwa trójkątów.

PrzyszlyMakler: Dobrze. Dziękuję Ci bardzo. Widzę podobieństwo kąt bok kąt, ale zawsze mnie ciekawiło− skąd wiadomo, który bok jest wprost proporcjonalny do którego? Otóż: [oznaczenia do rysunku Bogdana]

	h		y		h		h
skąd wiadomo, że		=		a nie np.		=
	x		h		x		y

Wiadomo, że na takim dużym ładnym rysunku to fizycznie niemożliwe, ale czasem może się zdarzyć, że różnie w bokach będą minimalne.

5-latek : . W trojkacie prostokątnym wysokość jest rowna sredniej geometrycznej odcinkow na jakie dzieli przeciwprostokatna Ty masz xu siebie to wysokość (bo pada pod katem prostym na przeciwprostokatna wiec x=√4*6

PrzyszlyMakler: Okej. Myślę, że zapamiętam, a odpowiecie jeszcze odnośnie tego powyższego postu między Metisem i 5−latkiem? Bo często w zadaniach z stereometrii trzeba szukać podobieństwa i nigdy nie wiem, który bok do którego..

notka: najlepiej pisać proporcje patrząc na kąty w trójkątach: na przeciw katów o równej mierze leżą boki proporcjonalne

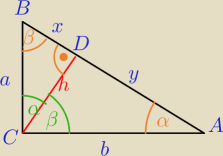
Mila: ΔADC∼ΔCDB⇔

y		h
	=		⇔
h		x

h²=x*y h=√x*y średnia geometryczna.

Mila: Często korzysta się z podobieństwa trójkątów.

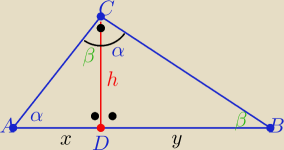
Eta: Z podobieństwa trójkątów ADC i BDC

h		y
	=		⇒ h2=xy ⇒ h=√xy
x		h

Eta:

PrzyszlyMakler: Jesteście cudowni!

PrzyszlyMakler: 1] Wielokątem, którego liczba przekątnych jest trzy razy większa od liczby wierzchołków jest: A] sześciokąt wypukły b] Ośmiokąt wypukły c] Dziewięciokąt wypukły Nie wiem jak zrobić to zadanie w inny sposób niż rysowanie, a to wydaje się być dośc prymitywne. 2] Liczbę log32 można przedstawić w postaci: a] log20 + log 12 b] 2log6 − log4 c] 4log8 d] 5log2

Eta:

	n(n−3)
1/		−−− liczba przekątnych wielokąta wypukłego , n−− ilość boków ( wierzchołków)
	2

(znasz ten wzorek? to n(n−3)=6n ⇒ n=9 Odp C)

Eta: 2/ 5 log2= log2⁵= ... odp; D) Jestem w <szoku> ,że o takie banały pytasz?

PrzyszlyMakler: Wiem. Ten logarytm to sam siebie zdziwiłem, bo był bardzo prosty :x. A tego wzorku z przekątnymi nie znałem. Dziękuję.

Eta: