Funkcja kwadratowa, ogarnie ktoś ? kJay: |x²+4x−5|+|x²+4x|=5

Godzio: x² + 4x = t |t − 5| + |t| = 5 Suma odległości od 5 i od 0 jest równa 5 Ponieważ 5 i 0 są od siebie oddalone o 5 to warunek jest spełniony dla dowolnego t z przedziału <0,5> 0 ≤ t ≤ 5 0 ≤ x² + 4x ≤ 5 0 ≤ x(x + 4) i x² + 4x − 5 ≤ 0 x ∊ (−∞,−4> U <0,∞) i (x + 5)(x − 1) ≤ 0 x ∊ <−5,1> Odp: x ∊ <−5,−4> U <0,1>

Eta:

kJay: Dzięki wielkie <3

Mila: 1) x²+4x−5≥0 Δ=16+20=36

	−4−6		−4+6
x=		=−5 lub x=		=1⇔
	2		2

x²+4x−5≥0 dla x≤−5 lub x≥1 stąd: |x²+4x−5|=x²+4x−5 dla x²+4x−5≥0 dla x≤−5 lub x≥1 |x²+4x−5|=−x²−4x+5 dla x∊(−5,1) 2) x²+4x≥0⇔x*(x+4)≥0⇔x<−4 lub x>0 |x²+4x|=x²+4x dla x<−4 lub x>0 |x²+4x|=−x²−4x dla x∊(−4,0) 3) rozważamy równanie w przedziałach 1) x≤−5 lub x≥1 obie funkcje maja wartości nieujemne x²+4x−5+x²+4x=5 2x²+8x−10=0 x²+4x−5=0 Δ=36 x=−5 lub x=1 należą do (−∞,−5>∪<1,∞) 2) x∊(−4,0) obie funkcje przyjmują wartości ujemne x²+4x−5+x²+4x=−5 2x²+8x=0 x²+4x=0 x=0 lub x=−4 liczby nie należą do przedziału (−4,0) 3) x∊(−5,−4> −x²−4x+5+x²+4x=5 5=5 każda liczba z przedziału (−5,−4) spełnia równanie 4) x∊<0,1) −x²−4x+5+x²+4x=5 5=5 każda liczba z przedziału <0,1) spełnia równanie Odpowiedź. 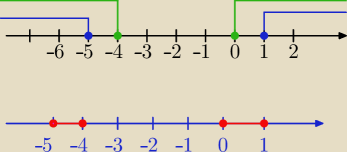x∊<−5,−4>∪<0,1>

kJay: Również dziękuję !

Mila: