oblicz wymiary xxxx: Ratownik majacy 100m line chce przy brzegu wytyczyc dla dzieci kapielisko ojak najwiekszym obszarze. Jakie wymiary powinno miec to kapielisko?

pipa: √100 =...

pipa: A z ilu stron ma być ogrodzone to kąpielisko

pipa: rozumiem, że było potrzebne na 8 do szkoły i już nieaktualne..

Mateusz: Masz 100m line dzieki tej informacji wiesz jaki bedzie obwód z zaleznosci obwodu wyznaczasz jedną zmienną i podstawiasz do wzoru na pole prostokąta, otrzymasz funkcje kwadratową wyznaczasz najwieksza wartosc tej funkcji

jc: Jeśli to prostokąt, to łatwo: a = część równoległa do brzegu b = każda z 2 prostopadłych częśći P = pole = ab, 100 = a + 2b 100/2 = (a + 2b)/2 ≥ √a 2b = √2 P stąd P ≤ 50² /2 = 1250, równość dla a = 50, b=25 Korzystamy z nierówności średnia arytmetyczna ≥ średnia geometryczna (x+y)/2 ≥ √xy, x, y ≥ 0

Jerzy: Jakie średnie ? 2x+2y =100 x + y = 50 y = 50 − x P = x*y = x(50−x) ....zwykły trójmian,który osiąga maksimum dla x = 25

Jerzy: Odp: kwadrat o boku 25 m

jc: Widziałeś kapieliska nad jeziorami? Przy brzegu nie ma liny. Więc raczej 2x+y = 100, P = x y = x ( 100 − 2x) = ...

Jerzy: No to: 2x + y = 100 y = 100 − 2x P = x(100 − 2x) ... i trójmian ma max dla x = 25 m

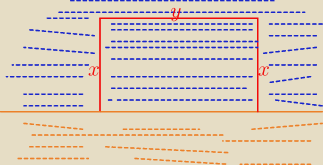
Eta: 2x+y=100 ⇒⇒ y= 100−2x i x∊(0,50)

	100
P= xy ⇒ P(x)= x*(100−2x) = −2x2+100x to xmax=		=25
	4

i y_max= 100−2x= 50 Wymiary kąpieliska o maksymalnym polu : y= 50 m i x= 25 m

Eta: