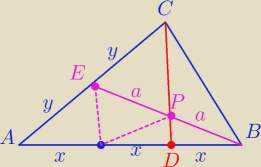
geometria mat: Dany jest trójkąt ABC oraz punkt D na jego boku AB taki, że |AD| = 2/3 |AB|. Z wierzchołka B poprowadzono środkowa˛ BE do boku AC. Punkt P jest punktem wspólnym odcinków CD i BE. Wykaż , że punkt P jest środkiem odcinka BE. Próbowałem ale nie umiem tego rozwiązać, bardzo proszę o pomoc

mat: Halo. halo

mat: Jeszcze raz proszę o pomoc

mat: Serio nikt, nie umie ?

Janek191:

Janek191: ? Tw. Talesa.

mat: A skąd pewność że te odcinki są równoległe

Janek191:

y		x
	= 1 =		więc PD II EF
y		x

mat: nie rozumiem tego, czemu

mat: dobra ok, już zrozumiałem, dziena

Janek191:

	I AE I		I AF I
Jeżeli		=		, to EF II CD .
	I EC I		I FD I

mat: no, ok linia środkowa trójkąta. Kompletnie tego nie zauważyłem. Jeszcze raz dzieki