W prawidłowym ostrosłupie czworokątnym
ola: W prawidłowym ostrosłupie czworokątnym kąt płaski przy wierzchołku jest równy α, zaś krawędź
podstawy ma długość a. Oblicz:
A. cosinus kata dwuściennego między ścianami bocznymi ostrosłupa
B. odległość wierzchołka podstawy od przeciwległej krawędzi bocznej.
29 lut 22:59
ola: proszę pomóżcie

29 lut 23:15
mat: cos2(α/2)−1/cos2(α/2)
29 lut 23:31
mat: masz odpowiedzi żeby sprawdzic czy dobry wynik


29 lut 23:38
ola: mat, mogłbys mi wytłumaczyć? bo nie rozumiem

29 lut 23:41
mat: Niech jeszcze ktoś sprawdzi podpunkt a i zobaczy czy tez tak wychodzi
29 lut 23:41
ola: nie

niestety
29 lut 23:41
mat: A odpowiedź jest dobra, możesz to sprawdzić

?
29 lut 23:42
ola: nie mam odpowiedzi do tych zadań właśnie

29 lut 23:44
mat: Ja to liczyłem tak że z tg(α/2) wyliczyłem wysokość boczną. Następnie znając tą wysokość pole
ściany bocznej.
Z sinusa(α/2) krawędź boczną. Z równości pół wyliczyłem prostopadłą do krawędzi bocznej.
Następnie znając dwie wysokości (do krawędzi bocznej) i przekątną podstawy z twierdzenia
cosinusów wyliczyłem kąt dwuścienny.
Ja to tak zrobiłem.
29 lut 23:45
Mila:
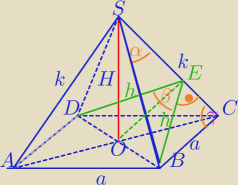
|DE|=|BE|=h
DE ⊥ SC i BE ⊥ SC
|DB|=a
√2
| | α | |
W ΔBCS: γ=(180−α):2=90− |
| |
| | 2 | |
| | α | | |BE| | | α | | |BE| | |
sin(90o− |
| = |
| ⇔cos |
| = |
| |
| | 2 | | a | | 2 | | a | |
W ΔDBE: z tw. cosinusów
|DB|
2=h
2+h
2−2*h*h *cosβ
(a
√2)
2=2h
2−2h
2*cosβ
a
2*2=2h
2*(1−cosβ)
| | α | |
2a2=2*a2*cos2 |
| *(1−cosβ) /:(2a2) |
| | 2 | |
| | α | | α | |
1=cos2 |
| *(1−cosβ) /:cos2 |
| |
| | 2 | | 2 | |
============
29 lut 23:50
ola: Mila i mat bardzo dziekuję za pkt. A
spróbuje zrobić i zrozumieć

29 lut 23:52
ola: a pkt B ktoś umie?

29 lut 23:52
mat: Czyli wyszło Tobie tak samo jak mi

W drugim mam
a
√1−2sin(α/2)/2
√2sin
2(α/2)
29 lut 23:53
mat: B liczyłem z podobieństwa trójkątów. Jeden trójkąt to wysokość ostrosłupa, połowa przekątnej i
krawędź boczna, a drugi to ten z odległością
29 lut 23:54
mat: @Mila wstawiłem na forum jedno zadanko z geomtrii, jakbyś mogła spojrzeć i spróbować pomóc

29 lut 23:56
ola: mat a powiesz dokładniej co do czego

?
w sensie jaka długość boku do jakiego

1 mar 00:04
Mila:
b) w ΔSBC:
a
2=k
2+k
2−2*k*k cosα
a
2=2k
2*(1−cosα)
W ΔSOC:
H
2+|OC|
2=k
2
| | a√2 | | a2 | |
H2+( |
| )2= |
| |
| | 2 | | 2*(1−cosα) | |
Teraz porównanie pól
x− szukana odległość A od krawędzi SC
1 mar 00:06
Mila:
Mat , chętnie ale jutro. Przypomnij się.
Ja policzyłam trochę (b) , jutro skończę. Dobranoc.
1 mar 00:06
ola: @Mila dziękuję

1 mar 00:11




 niestety
niestety
 ?
?

 |DE|=|BE|=h
DE ⊥ SC i BE ⊥ SC
|DB|=a√2
|DE|=|BE|=h
DE ⊥ SC i BE ⊥ SC
|DB|=a√2


 W drugim mam
a√1−2sin(α/2)/2√2sin2(α/2)
W drugim mam
a√1−2sin(α/2)/2√2sin2(α/2)

 ?
w sensie jaka długość boku do jakiego
?
w sensie jaka długość boku do jakiego 
