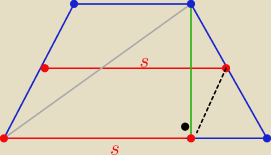
asd olekturbo: W okrąg o promieniu 13 wpisano trapez, gdzie dłuższa podstawa trapezu jest średnicą okręgu. Przekątna trapezu wynosi 24. Oblicz odcinka łączącego środki ramion. Dobrze to robie?

24
	= 26
sina

	12
sina =
	13

sin²a+cos²a = 1

	5
cosa =
	13

	12
tga =
	5

h		12
	=
x		5

12x = 5h

	12
h =		x
	5

(26−x)² + h² = 24²

	144
(26−x)2 +		x2 = 242
	25

	144
676 − 52x + x2 +		x2 = 576
	25

169
	x2−52x+100 = 0
25

169x²−1300x+2500 = 0 Δ = 1 690 000 − 1 690 000 = 0

	1300
x0 =
	338

	26−2x+26
s =
	2

olekturbo: ref

Eta: c=√26²−24²= 10

	24*10		120
h=		=
	26		13

	a+b		288
|AE|=s=		= √242−h2= ...=
	2		13

olekturbo: Czyli źle. Ale co źle zrobiłem?

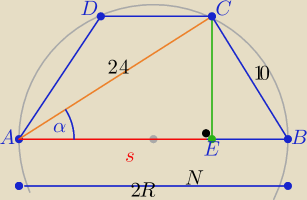Eta: 2 sposób c=10 z twierdzenia sinusów w ΔABC:

	10		5		12
		=2R=26 ⇒ sinα=		to cosα=
	sinα		13		13

	288
W ΔAEC : s= 24*cosα=
	13

olekturbo: Dzieki

Eta:

Eta: Powodzenia w następnych zadaniach z trapezami

Eta: Nie wiem co źle obliczyłeś, bo nie chce mi się czytać takiego "tasiemca"

olekturbo:

Eta:

Eta: Takie miliony w delcie by mi się przydały