czworościan foremny trudne
kiniaa: Czworościan foremny przecięto płaszczyzną przechodzącą przez krawędź podstawy oraz środek
przeciwległej krawędzi bocznej. Oblicz cosinus kąta zawartego między płaszczyzną a podstawą
ostrosłupa.
potrafi ktoś pomóc?
29 lut 19:24
kiniaa: pomocy

1 mar 19:38
mat: podstawa tego przekroju to bok a, a ramiona to a
√3/2, bo przecinają się w połowie. Z tego
wyliczas pitagorasem wysokość przekroju. Mając wysokość rysujesz sobie trójkąt którego jednym
z boków jest ta wysokość, drugim wysokosć podstawy, a trzeci to połowa krawędzi bocznej czyli
a/2. I tw cosinusów liczy odpowiedni cosinus.

1 mar 19:45
mat: jak masz odpowiedź do tego zadanka to podaj ją jakbyś mogła
1 mar 19:46
mat: Według mnie powinno wyjść √6/3
1 mar 19:52
kiniaa: właśnie nie mam żadnej odpowiedzi, a kompletnie nie wiem jak się do tego zabrać

1 mar 20:18
kiniaa: ale dziękuję za pomoc

1 mar 20:19
Mila:
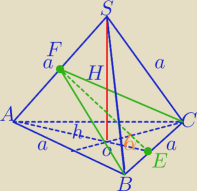
WΔFEC:
W ΔAEF:
|AF|
2=h
2+|FE|
2−2*h*|FE|*cosα
| a2 | | 3a2 | | a2 | | α√3 | | a | |
| = |
| + |
| −2* |
| * |
| *cosα /:a2 |
| 4 | | 4 | | 2 | | 2 | | √2 | |
===========
1 mar 22:16




