
 z tw. Talesa
|AB|=2|RQ|
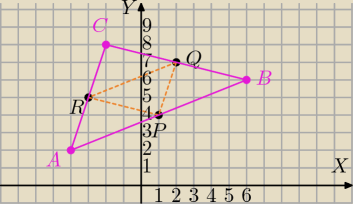
RQ→=[5;2] po przesunięciu punktu P o wektor RQ otrzymamy Punkt B
P=(1;4)→T[5;2]→B=(1+5;4+2)=(6;6)
P(1;4)→T[−5;−2]→A=(−4;2)
Wsp. punktu C możesz znaleźć, korzystając z tego, że Q jest środkiem BC
lub,że R środkiem AC.
Q=(2;7)
z tw. Talesa
|AB|=2|RQ|
RQ→=[5;2] po przesunięciu punktu P o wektor RQ otrzymamy Punkt B
P=(1;4)→T[5;2]→B=(1+5;4+2)=(6;6)
P(1;4)→T[−5;−2]→A=(−4;2)
Wsp. punktu C możesz znaleźć, korzystając z tego, że Q jest środkiem BC
lub,że R środkiem AC.
Q=(2;7)
| 6+cx | ||
2= | ⇔6+cx=4⇔cx=−2 | |
| 2 |
| 6+cy | ||
7= | ⇔6+cy=14 | |
| 2 |