geometria analityczna/funkcja kwadratowa Ergo: Odcinek AB o koncach A(−2,−1) i B(2,3) jest podstawa trojkata ABC. Wierzcholek C nalezy do wykresu funkcji f(x)=x²+6x+10. Wyznacz wspolrzedne punktu C, aby pole trojkata ABC bylo najmniejsze. Ile ono wynosi. no to tak : wyznaczam prosta AB : y=x+1 i domyslam sie ze trzeba skorzystac ze wzoru na odleglosc od punktu, bo zeby pole bylo najmniejsze to odleglosc musi byc najmniejsza. Nie wiem jak to wykorzystac. Prosze o pomoc

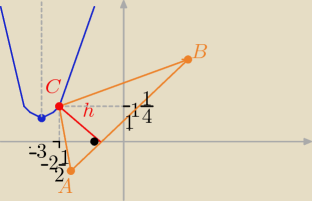
Eta: Prosta zawierająca podstawę AB ma równanie: ( y −y_A)( x_B−x_A)= ( x −x_A)(y_B−y_A) po podstawieniu i uporzadkowaniu otrzymasz: pr. AB: y = x +1 równanie ogólne: x −y +1=0 C( x, y) i y= x² +6x +10 odległość C od prostej AB musi być najmniejsza: czyli h−−− najmniejsze wyznaczamy tę odległość:

	Ix*1 −1*y +1I
d= h=
	√2

teraz należy opuścić moduł , widać z rys.,że punkt C(x,y) leży na paraboli powyżej prostej AB więc y > x +1 => x −y +1 <0 zatem opuszczając moduł zmieniamy znaki:

	−x +y −1
h=		i y= x2 +6x +10
	√2

otrzymamy:

	1		1
h(x) =		( −x +x2 +6x +10 −1) =		( x2 +5x +9)
	√2		√2

	−b		−5
zatem minimum osiaga dla xmin=		=		= −212
	2a		2

to y_min= (⁻⁵₂)²+ 6*(−⁵₂)+10 = 1¹₄ zatem C( −2¹₂, 1¹₄)

	I−52*1 −54+1I		11		11√2
wartość pola jest h=		=		=
	√2		4√2		8

IABI= √16+16= 4√2

	11√2		11
to P= 12*		*4√2=		= 512 [ j2]
	8		2

mam nadzieję ,że się nie pomyliłam w rachunkach .... sprawdzaj

Ergo: wszystko sie zgadza bardzo dziekuje za poswiecony czas i wreszcie pojalem to

cj z gta andrass: ćw 14 str 134 "MATEMATYKA 1 Z PLUSEM " ciołku to zadanie

ZK: Odezwal sie Brus Wszechwiedzacy

sandra: ^x+1_4x={1}{x−1}

ZK:

x+1		1
	=		zal. 4x≠0 i x−1≠0
4x		x−1

Mnozenie na krzyz (x+1)(x−1)=1*4x x²−1=4x bo ze wzoru skroconego mnozenia a²−b²=(a+b)(a−b) x²−4x−1=0 a to juz potrafisz rozwiazac −zwykle rownanie kwadratowe i na koncu sprawdzasz z zalozeniem