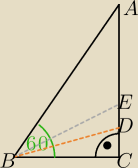
 BC = x, AC = x*√3
∡ABC = 600
∡BAC = 300
∡ABE = 300
∡BEA = 1800 − ∡BAE − ∡ABE = 1800 − 300 − 300 = 1200
∡BEC = 1800 − ∡BEA = 1800 − 600 = 1200
tg(∡BEC) = tg600 = √3
BC = x, AC = x*√3
∡ABC = 600
∡BAC = 300
∡ABE = 300
∡BEA = 1800 − ∡BAE − ∡ABE = 1800 − 300 − 300 = 1200
∡BEC = 1800 − ∡BEA = 1800 − 600 = 1200
tg(∡BEC) = tg600 = √3
| BC | ||
tg(∡BEC) = | ||
| EC |
| x | ||
√3 = | ||
| EC |
| x | ||
EC = | ||
| √3 |
| EC | ||
tg(300) = | ||
| BC |
| x/√3 | ||
tg(300) = | ||
| x |
| x | 1 | |||
tg(300) = | * | |||
| √3 | x |
| √3 | ||
tg(300) = | ||
| 3 |

 1) w Δrównobocznym
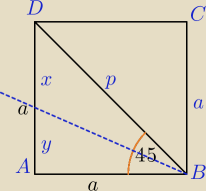
2) Kwadrat
1) w Δrównobocznym
2) Kwadrat
| y | ||
tg( 22.5)= | ||
| a |
| a | a√2 | ||
= | |||
| y | x |
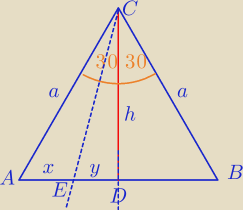 h=0.5√3
1) CD jest dwusieczną kąta ACB.
h=0.5√3
1) CD jest dwusieczną kąta ACB.
| 0.5a | 1 | |||
tg(300)= | = | |||
| 0.5a√3 | √3 |
| a | h | a | 0.5a√3 | ||||
= | ⇔ | = | ⇔ | ||||
| x | y | x | y |
| 1 | 0.5√3 | ||
= | |||
| x | y |
| a | ||
x+y= | ||
| 2 |
| y | ||
tg(15)= | ||
| h |
| y | x | ||
= | |||
| a | a√2 |
| x+y | (x+y)√2 | ||
= | |||
| y | x |
 \
Milu w poscie z 23:41 mogę przyjąć ze
\
Milu w poscie z 23:41 mogę przyjąć ze
| 1 | 1 | |||
x+y=a i x= | a a także y= | a | ||
| 2 | 2 |
| y | x | ||
= | |||
| a | a√2 |
| 0,5a | 0,5a | ||
= | |||
| a | a√2 |
| x | ||
y= | ||
| √2 |


| a | ||
y= | ||
| (√2+1) |
| y | a(√2−1) | |||
to tg22o30')= | = | = √2−1 | ||
| a | a |
| y | ||
tg(15o)= | ||
| h |
| 1 | 0.5√3 | ||
= | ⇔y=0.5*√3*x | ||
| x | y |
| a | ||
x= | −y | |
| 2 |
| a | ||
y=0.5√3*( | −y) | |
| 2 |
| a√3 | 1 | |||
y= | − | √3*y | ||
| 4 | 2 |
| 1 | a√3 | |||
y+ | √3*y= | |||
| 2 | 4 |
| √3 | a√3 | |||
y*(1+ | )= | /*4 | ||
| 2 | 4 |
| a√3*(4−2√3) | ||
y= | ||
| 4 |
| a√3*(4−2√3) | 2 | |||
tg(15o)= | * | |||
| 4 | a√3 |
 Miałem kłopoty wlasnie z dokonczenien
Miałem kłopoty wlasnie z dokonczenien 
